题目内容
19.在平行四边形ABCD中,$\overrightarrow{AC}•\overrightarrow{CB}=0$,$2{\overrightarrow{BC}^2}+{\overrightarrow{AC}^2}-4=0$,若将其沿AC折成直二面角D-AC-B,则三棱锥D-ACB的外接球的表面积为( )| A. | 16π | B. | 8π | C. | 4π | D. | 2π |
分析 由已知中$\overrightarrow{AC}•\overrightarrow{CB}=0$,可得AC⊥CB,沿AC折成直二面角D-AC-B,平面DAC⊥平面ACB,可得三棱锥A-BCD的外接球的直径为BD,进而根据$2{\overrightarrow{BC}^2}+{\overrightarrow{AC}^2}-4=0$,求出三棱锥D-ACB的外接球的半径,可得三棱锥D-ACB的外接球的表面积.
解答 解:平行四边形ABCD中,
∵$\overrightarrow{AC}•\overrightarrow{CB}=0$,
∴AC⊥CB,
沿AC折成直二面角D-AC-B,∴平面DAC⊥平面ACB,
三棱锥D-ACB的外接球的直径为DB,
∴BD2=AD2+AC2+BC2=2BC2+AC2=4
∴外接球的半径为1,
故表面积是4π.
故选:C.
点评 本题考查的知识点是球内接多面体,平面向量数量积的运算,其中根据已知求出三棱锥D-ACB的外接球的半径是解答的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
7.已知$p:\frac{1}{x-2}≥1$,q:|x-a|<1.若q是p的必要不充分条件,则实数a的取值范围是( )
| A. | (2,3] | B. | [2,3] | C. | (2,3) | D. | (-∞,3] |
14.哈尔滨市投资修建冰雪大世界,为了调查此次修建冰雪大世界能否收回成本,组委会成立了一个调查小组对国内参观冰雪大世界的游客的消费指数(单位:百元)进行调查,在调查的1000位游客中有100位哈尔滨本地游客,把哈尔滨本地游客记为A组,内外地游客记为B组,按分层抽样从这1000人中抽取A,B组人数如下表:
A组:
B组:
(1)确定a的值,再分别在答题纸上完成A组与B组的频率分布直方图;
(2)分别估计A,B两组游客消费指数的平均数,并估计被调查的1000名游客消费指数的平均数.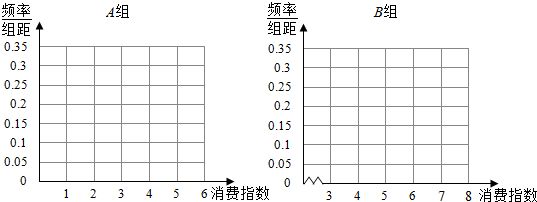
A组:
| 消费指数(百元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
| 人数 | 3 | 4 | 6 | 5 | 2 |
| 消费指数(百元) | [3,4) | [4,5) | [5,6) | [6,7) | [7,8] |
| 人数 | 9 | 36 | a | 54 | 9 |
(2)分别估计A,B两组游客消费指数的平均数,并估计被调查的1000名游客消费指数的平均数.

8.在长方体ABCD-A1B1C1D1中,AB=6,BC=4,AA1=2,P,Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为( )
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{34}$ | D. | 5$\sqrt{2}$ |
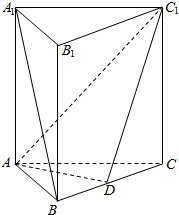 如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.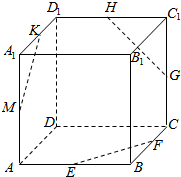 已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.
已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.