题目内容
11.函数f(x)=-x2+2ax+1,x∈[0,4],(1)当a=1时,求函数f(x)的最值;
(2)求函数f(x)的值域.
分析 配方可得f(x)=-x2+2ax+1=-(x-a)2+a2+1:
(1)当a=1时,f(x)=-(x-1)2+2,易得二次函数的最值;
(2)由二次函数的单调性和对称轴的关系,分类讨论可得.
解答 解:配方可得f(x)=-x2+2ax+1=-(x-a)2+a2+1,
(1)当a=1时,f(x)=-(x-1)2+2,
∴当x∈[0,1]时,函数f(x)单调递增,
当x∈[1,4]时,函数f(x)单调递减,
∴当x=1时,函数取最大值2,
当x=4时,函数取最小值-7;
(2)当a≤0时,函数f(x)在x∈[0,4]上单调递减,
∴当x=0时,函数取最大值1,当x=4时,函数取最小值8a-15,
∴函数的值域为[8a-15,1];
当a≥4时,函数f(x)在x∈[0,4]上单调递增,
∴当x=0时,函数取最小值1,当x=4时,函数取最大值8a-15,
∴函数的值域为[1,8a-15];
当0<a<2时,函数f(x)在x∈[0,a]上单调递增,在x∈[a,4]上单调递减,
∴当x=a时,函数取最大值a2+1,当x=4时,函数取最小值8a-15,
∴函数的值域为[8a-15,a2+1];
当2≤a<4时,函数f(x)在x∈[0,a]上单调递增,在x∈[a,4]上单调递减,
∴当x=a时,函数取最大值a2+1,当x=0时,函数取最小值1,
∴函数的值域为[1,a2+1].
点评 本题考查二次函数的值域,涉及分类讨论的思想和数形结合,属中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
1.已知一个算法,其流程图如图所示,则输出结果是( )


| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
3.设函数f(x)=|3x-1|,c<b<a,且f(c)>f(a)>f(b),则下列关系中一定成立的是( )
| A. | 3c+3a=2 | B. | 3c+3a>2 | ||
| C. | 3c+3a<2 | D. | 3c+3a与2的大小关系不确定 |
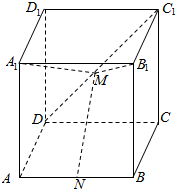 如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.
如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.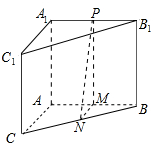 在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.
在三棱锥ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M,N,P分别是棱AB,BC,B1C1的中点.