题目内容
9.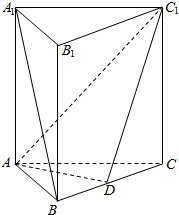 如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.(1)求证:平面C1AD⊥平面B1BCC1:
(2)求证:A1B∥平面C1AD.
分析 (1)推导出AD⊥C1D,AD⊥CC1,由此能证明平面C1AD⊥平面B1BCC1.
(2)连结A1C,交AC1于O,连结OD,推导出OD∥A1B,由此能证明A1B∥平面C1AD.
解答 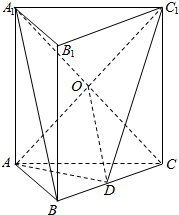 证明:(1)∵在正三棱柱ABC-A1B1C1中,点D在棱BC上,
证明:(1)∵在正三棱柱ABC-A1B1C1中,点D在棱BC上,
AD⊥C1D,AD⊥CC1,C1D∩CC1=C1,
∴AD⊥平面B1BCC1,
∵AD?平面C1AD,
∴平面C1AD⊥平面B1BCC1.
(2)连结A1C,交AC1于O,连结OD,
∵正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
平面C1AD⊥平面B1BCC1,
∴D是BC中点,O是A1C中点,
∴OD∥A1B,
∵A1B?平面C1AD,OD?平面C1AD,
∴A1B∥平面C1AD.
点评 本题考查面面垂直和线面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
19.若sinα<0,cosα<0,则α所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.若椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{1}{2}$,则双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的离心率是( )
| A. | 2 | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 3 |
1.已知一个算法,其流程图如图所示,则输出结果是( )


| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
18.一个正方体的棱长为2cm,它的顶点都在一个球面上,则球的半径是( )cm.
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |