题目内容

已知
a
=（2，4，x），
b
=（2，y，2），若|
a
|=6，
a
⊥
b
，则x+y的值是（　　）
A、-3或1B、3或-1
C、-3D、1
考点：平面向量数量积的运算
专题：计算题,空间向量及应用
分析：运用向量的模的公式，可得x，再由向量垂直的条件：数量积为0，可得y，进而得到x+y的值．
解答： 解：由
a
=（2，4，x），|
a
|=6，
则
4+16+x2
=6，解得x=±4，
又
b
=（2，y，2），且
a
⊥
b
，
则
a
•
b
=0，即有4+4y+2x=0，
即y=-
x+2
2
．
当x=4时，y=-3，有x+y=1；
当x=-4时，y=1，有x+y=-3．
故选A．
点评：本题考查空间向量的数量积的性质，考查向量的模的公式，考查向量垂直的条件，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知α，β∈(
π
2
，π)，M（Rcosα，Rsinα），N（Rcosβ，Rsinβ），则直线MN的倾斜角为
 
．
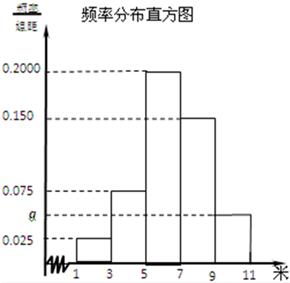为了解高一年级女生的身体状况，从该高一年级女生中抽取一部分进行“掷铅球”的项目测试，把获得的数据分成[1，3）[3，5）[5，7）[7，9）[9，11）五组（假设测试成绩都不超过11米），画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
（1）求实数a的值及参加“掷铅球”项目测试的人数；
（2）若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试，求所抽取的2名学生自不同组的概率．
a，b，c分别为△ABC三个内角A，B，C的对边，bcosC+
3
bsinC-a-c=0
（1）求证A，B，C成等差数列；
（2）若a=2，△ABC的面积为
3
，求b，c；
（3）若a，b，c成等比数列，求sinAsinC的值；
（4）求sinA+sinC的取值范围；
（5）若b=
3
，求2a+c的最大值．
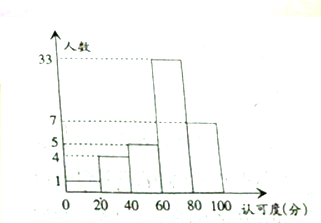某校为了了解新的一轮教改模式有效性的“认可度”，在全校师生（可认为很多人）进行了“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”统计分析得如图
（1）求这50名师生的“认可度”的平均值（每一区间取中点值计算）
（2）设表中个区间“认可度”分数的中点值构成集合A，那么从集合A中任取一值，记下该值后放回，然后再随机任选一个又记下该值后又放回，设第一次的值记为x，第二次的值记为y，求y＞x的概率．
函数f（x）=ax+1，（a＞0且a≠1）
（1）当a=3，x∈[-1，2]时，求函数f（x）的值域；
（2）求不等式f（x）≥1的解集．
函数f（x）=
log2(1-x)-2a，x≤0
x2-4ax+a，x＞0
有三个不同零点，则实数a的取值范围是（　　）
A、a≤0
B、a＞
1
4
C、
1
4
＜a≤
1
2
或a＜0
D、a＞
1
4
或a＜0
已知函数f（x）=mx3-x．
（1）讨论单调区间；
（2）m=1时，求曲线f（x）在M（t，f（t））处的切线方程；
（3）m=1时，设a＞0，如果过点（a，b）时做曲线f（x）的三条切线，证明-a＜b＜f（a）
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右顶点和右焦点分别为A（a，0）、F（c，0），若在直线x=-
a2
c
上存在点P使得∠APF=30°．则该双曲线的离心率的取值范围是（　　）
A、（1，
3+
17
2
]
B、[
3+
17
2
，+∞）
C、（1，4]
D、[4，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网