题目内容
已知双曲线
-
=1(a>0,b>0)的右顶点和右焦点分别为A(a,0)、F(c,0),若在直线x=-
上存在点P使得∠APF=30°.则该双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
A、(1,
| ||||
B、[
| ||||
| C、(1,4] | ||||
| D、[4,+∞) |
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:首先运用正弦定理,求得圆的半径r=c-a,再由直角三角形求得圆B的方程,所求圆恰好经过A,F,则原题等价于直线x=-
与圆B存在公共点,即有
+
≤c-a,由离心率公式,解不等式即可得到.
| a2 |
| c |
| a+c |
| 2 |
| a2 |
| c |
解答:
解:由A(a,0)、F(c,0),
则|AF|=c-a,
由正弦定理可得,2r=
=2(c-a),即有r=c-a,
且圆心B在x=
上,
当△AFQ为直角三角形,且∠AQF=30°,∠QAF=90°时,可得B的纵坐标为
(c-a).
故以B(
,
)为圆心、c-a为半径的圆B恰好经过A、F两点,
且圆B上的点Q即为使得∠AQF=30°的所有点,
所以原题等价于直线x=-
与圆B存在公共点,
即
+
≤c-a⇒e2-3e-2≥0
⇒e≥
,或e≤
(舍去).
故选B.
则|AF|=c-a,
由正弦定理可得,2r=
| |AF| |
| sin30° |
且圆心B在x=
| a+c |
| 2 |
当△AFQ为直角三角形,且∠AQF=30°,∠QAF=90°时,可得B的纵坐标为
| ||
| 2 |
故以B(
| a+c |
| 2 |
| ||
| 2 |
且圆B上的点Q即为使得∠AQF=30°的所有点,
所以原题等价于直线x=-
| a2 |
| c |
即
| a+c |
| 2 |
| a2 |
| c |
⇒e≥
3+
| ||
| 2 |
3-
| ||
| 2 |
故选B.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查直线和圆的关系,考查正弦定理的运用,考查运算能力,属于中档题和易错题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知
=(2,4,x),
=(2,y,2),若|
|=6,
⊥
,则x+y的值是( )
| a |
| b |
| a |
| a |
| b |
| A、-3或1 | B、3或-1 |
| C、-3 | D、1 |
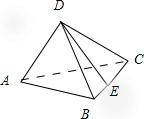 在四面体ABCD中,已知
在四面体ABCD中,已知| AB |
| b |
| AD |
| a |
| AC |
| c |
| BE |
| 1 |
| 2 |
| EC |
| DE |
A、-
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
在四边形ABCD中,M、N分别是AD和BC的中点,则向量
=( )
| MN |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|