题目内容

函数f（x）=
log2(1-x)-2a，x≤0
x2-4ax+a，x＞0
有三个不同零点，则实数a的取值范围是（　　）
A、a≤0
B、a＞
1
4
C、
1
4
＜a≤
1
2
或a＜0
D、a＞
1
4
或a＜0
考点：函数零点的判定定理
专题：计算题,函数的性质及应用
分析：分析分段函数可知，函数在两段上都要达到最多解才可以有三个，从而解得．
解答： 解：函数f（x）=
log2(1-x)-2a，x≤0
x2-4ax+a，x＞0
有三个不同零点，
∴当x≤0时，log2（1-x）=2a有一个解，
故a=
1
2
log2（1-x）≥0；
当x＞0时，x2-4ax+a=0有两个不同的解；
故
△=(4a)2-4a＞0
4a＞0
a＞0
；
解得，a＞
1
4
；
综上所述，a＞
1
4
；
故选：B．
点评：本题考查了函数的零点与方程的根的联系与应用，属于基础题．
练习册系列答案
相关题目
∫
3
-3
（x2-2sinx）dx=
 
．
若函数f（x）和g（x）满足：①在区间[a，b]上均有定义；②函数y=f（x）-g（x）在区间[a，b]上至少有一个零点，则称f（x）和g（x）在[a，b]上具有关系G．
（1）若f（x）=lgx，g（x）=3-x，试判断f（x）和g（x）在[1，4]上是否具有关系G，并说明理由；
（2）若f（x）=2|x-2|+1和g（x）=mx2在[1，4]上具有关系G，求实数m的取值范围．
已知
a
=（2，4，x），
b
=（2，y，2），若|
a
|=6，
a
⊥
b
，则x+y的值是（　　）
A、-3或1B、3或-1
C、-3D、1
已知|
a
|=4，|
b
|=2，且
a
与
b
的夹角为120°，求
（1）|
a
+
b
|；
（2）若（
a
+λ
b
）⊥（2
a
-3
b
），求λ的值．
已知圆C的圆心在直线y=x-1上，且A（2，0），B（
9
5
，
3
5
）在圆C上．
（1）求圆C的方程；
（2）若圆M：x2+（y-2
2
）2=r2（r＞0）与圆C相切．求直线y=
7
x截圆M所得弦长．
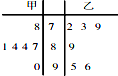甲乙两同学在高二年级的6次数学测验成绩（满分100分）如图茎叶图所示，则下列说法正确的是（　　）
A、甲乙同学的平均成绩相同，但是甲同学的成绩比乙稳定
B、甲乙同学的平均成绩相同，但是乙同学的成绩比甲稳定
C、甲同学的平均成绩比乙同学好，但是乙同学的成绩比甲稳定
D、乙同学的平均成绩比甲同学好，但是甲同学的成绩比乙稳定
已知圆C：x2+y2+Dx+Ey+3=0，圆C关于直线x+y-1=0对称，圆心在第二象限，半径为
2
．
（1）求圆C的方程；
（2）已知不过原点的直线l与圆C相切，且与x轴、y轴上的截距相等，求直线l的方程．
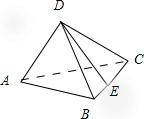在四面体ABCD中，已知
AB
=
b
，
AD
=
a
，
AC
=
c
，
BE
=
1
2
EC
，则
DE
=（　　）
A、-
a
+
2
3
b
+
1
3
c
B、
a
+
2
3
b
+
1
3
c
C、
a
-
2
3
b
+
1
3
c
D、
2
3
a
-
b
+
1
3
c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网