题目内容
已知函数f（x）=mx3-x．
（1）讨论单调区间；
（2）m=1时，求曲线f（x）在M（t，f（t））处的切线方程；
（3）m=1时，设a＞0，如果过点（a，b）时做曲线f（x）的三条切线，证明-a＜b＜f（a）
（1）讨论单调区间；
（2）m=1时，求曲线f（x）在M（t，f（t））处的切线方程；
（3）m=1时，设a＞0，如果过点（a，b）时做曲线f（x）的三条切线，证明-a＜b＜f（a）
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题：计算题,证明题,导数的综合应用
分析：（1）求导f′（x）=3mx2-1，从而讨论导数的正负以确定函数的单调性；
（2）m=1时，f′（x）=3x2-1，从而可得f′（t）=3t2-1，f（t）=t3-t，从而写出切线方程；
（3）结合（2）知，过点（a，b）的切线满足b=（3t2-1）a-2t3；从而化为方程2t3-3at2+a+b=0有三个不同的实数根，从而由数形结合的思想求解．
（2）m=1时，f′（x）=3x2-1，从而可得f′（t）=3t2-1，f（t）=t3-t，从而写出切线方程；
（3）结合（2）知，过点（a，b）的切线满足b=（3t2-1）a-2t3；从而化为方程2t3-3at2+a+b=0有三个不同的实数根，从而由数形结合的思想求解．
解答：
解：（1）f′（x）=3mx2-1，
①当m≤0时，f′（x）=3mx2-1＜0恒成立，
故函数f（x）=mx3-x在R上是减函数；
②当m＞0时，
当x∈（-∞，-
）∪（
，+∞）时，f′（x）＞0；
当x∈（-
，
）时，f′（x）＜0；
故f（x）的单调增区间为（-∞，-
），（
，+∞）；
单调减区间为（-
，
）；
（2）m=1时，
f′（x）=3x2-1，
f′（t）=3t2-1，f（t）=t3-t，
故切线方程为y-（t3-t）=（3t2-1）（x-t）；
化简得，y=（3t2-1）x-2t3；
（3）证明：由（2）知，过点（a，b）的切线满足
b=（3t2-1）a-2t3；
即方程2t3-3at2+a+b=0有三个不同的实数根，
记g（t）=2t3-3at2+a+b，
则g（t）=6t2-6at=6t（t-a），
故g（t）在t=0处有极大值a+b；在t=a处有极小值b-f（a）；
故由题意可得，
b-f（a）＜0＜a+b；
即-a＜b＜f（a）．
①当m≤0时，f′（x）=3mx2-1＜0恒成立，
故函数f（x）=mx3-x在R上是减函数；
②当m＞0时，
当x∈（-∞，-
| ||
| 3m |
| ||
| 3m |
当x∈（-
| ||
| 3m |
| ||
| 3m |
故f（x）的单调增区间为（-∞，-
| ||
| 3m |
| ||
| 3m |
单调减区间为（-
| ||
| 3m |
| ||
| 3m |
（2）m=1时，
f′（x）=3x2-1，
f′（t）=3t2-1，f（t）=t3-t，
故切线方程为y-（t3-t）=（3t2-1）（x-t）；
化简得，y=（3t2-1）x-2t3；
（3）证明：由（2）知，过点（a，b）的切线满足
b=（3t2-1）a-2t3；
即方程2t3-3at2+a+b=0有三个不同的实数根，
记g（t）=2t3-3at2+a+b，
则g（t）=6t2-6at=6t（t-a），
故g（t）在t=0处有极大值a+b；在t=a处有极小值b-f（a）；
故由题意可得，
b-f（a）＜0＜a+b；
即-a＜b＜f（a）．
点评：本题考查了导数的综合应用及数形结合的思想应用，属于中档题．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知
=（2，4，x），
=（2，y，2），若|
|=6，
⊥
，则x+y的值是（ ）
| a |
| b |
| a |
| a |
| b |
| A、-3或1 | B、3或-1 |
| C、-3 | D、1 |
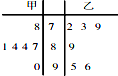甲乙两同学在高二年级的6次数学测验成绩（满分100分）如图茎叶图所示，则下列说法正确的是（ ）| A、甲乙同学的平均成绩相同，但是甲同学的成绩比乙稳定 |
| B、甲乙同学的平均成绩相同，但是乙同学的成绩比甲稳定 |
| C、甲同学的平均成绩比乙同学好，但是乙同学的成绩比甲稳定 |
| D、乙同学的平均成绩比甲同学好，但是甲同学的成绩比乙稳定 |