题目内容
已知集合A={x||x|<3},B={x|y=lg(x-1)},则集合A∩B为( )
| A、[0,3) |
| B、[1,3) |
| C、(1,3) |
| D、(-3,1] |
考点:对数函数的定义域,交集及其运算
专题:集合
分析:根据绝对值和对数函数求出集合A和B,然后由交集的定义求出结果.
解答:
解:∵|x|<3
∴-3<x<3
故A=(-3,3)
∵y=lg(x-1)
∴x-1>0,解得x>1
故B=(1,+∞)
∴A∩B=(1,3)
故选:C.
∴-3<x<3
故A=(-3,3)
∵y=lg(x-1)
∴x-1>0,解得x>1
故B=(1,+∞)
∴A∩B=(1,3)
故选:C.
点评:本题考查交集的定义的运算,是基础题.解题时要认真审题,注意含绝对值不等式和对数函数的性质的灵活运用.

练习册系列答案
相关题目
执行如图所示的程序框图后,输出的值为4,则P的取值范围是( )


A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
设f(x)是定义在[-6,6]上的偶函数,且f(4)>f(1),则下列各式一定成立的是( )
| A、f(0)<f(6) |
| B、f(4)>f(3) |
| C、f(2)>f(0) |
| D、f(-1)<f(4) |
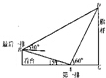 某中学举行升旗仪式,如图所示,在坡度为15°的看台上,从正对旗杆的一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离AB=10
某中学举行升旗仪式,如图所示,在坡度为15°的看台上,从正对旗杆的一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离AB=10