题目内容
已知椭圆C的焦点与双曲线
-x2=1的顶点重合，椭圆C的长轴长为4．
（1）求椭圆C的标准方程；
（2）若已知直线y=x+m，当m为何值时，直线y=x+m与椭圆C有公共点？
| y2 |
| 3 |
（1）求椭圆C的标准方程；
（2）若已知直线y=x+m，当m为何值时，直线y=x+m与椭圆C有公共点？
考点：直线与圆锥曲线的关系
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：（1）求出双曲线的顶点，得到c=
，椭圆C的长轴长为4，则有a=2，即有b=1．即可得到椭圆方程；
（2）联立直线y=x+m和椭圆方程，消去y，得到5x2+8mx+4m2-4=0，当判别式△≥0时，直线y=x+m与椭圆C有公共点．解出不等式即可．
| 3 |
（2）联立直线y=x+m和椭圆方程，消去y，得到5x2+8mx+4m2-4=0，当判别式△≥0时，直线y=x+m与椭圆C有公共点．解出不等式即可．
解答：
解：（1）双曲线
-x2=1的顶点为（0，±
），
则椭圆C的焦点为（0，±
），则c=
，
椭圆C的长轴长为4，则有a=2，即有b=1．
则椭圆C的标准方程为：
+y2=1；
（2）联立直线y=x+m和椭圆方程，消去y，得到
5x2+8mx+4m2-4=0，
当判别式△≥0时，直线y=x+m与椭圆C有公共点．
即有（8m）2-4×5×（4m2-4）≥0，
解得，-
≤m≤
故当m∈[-
，
]，直线y=x+m与椭圆C有公共点．
| y2 |
| 3 |
| 3 |
则椭圆C的焦点为（0，±
| 3 |
| 3 |
椭圆C的长轴长为4，则有a=2，即有b=1．
则椭圆C的标准方程为：
| x2 |
| 4 |
（2）联立直线y=x+m和椭圆方程，消去y，得到
5x2+8mx+4m2-4=0，
当判别式△≥0时，直线y=x+m与椭圆C有公共点．
即有（8m）2-4×5×（4m2-4）≥0，
解得，-
| 5 |
| 5 |
故当m∈[-
| 5 |
| 5 |
点评：本题考查椭圆和双曲线的方程和性质，考查直线和椭圆的位置关系，考查运算能力，属于中档题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
已知集合A={x||x|＜3}，B={x|y=lg（x-1）}，则集合A∩B为（ ）
| A、[0，3） |
| B、[1，3） |
| C、（1，3） |
| D、（-3，1] |
已知函数f（x）=x2-2x+2，的定义域与值域均为[1，b]，则b=（ ）
| A、3 | B、2或3 | C、2 | D、1或2 |
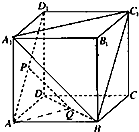如图，在棱长为a的正方体ABCD-A1B1C1D1中，P、Q分别是AD1、BD的中点．