题目内容
若函数f(x)=x+
(b∈R)的导函数在区间(1,2)上有零点,则b的取值范围是( )
| b |
| x |
| A、(4,+∞) |
| B、(-∞,1) |
| C、(1,+∞) |
| D、(1,4) |
考点:导数的运算,函数零点的判定定理
专题:导数的概念及应用
分析:先求导,在根据零点的存在定理,求出b的范围
解答:
解:∵f(x)=x+
(b∈R),
∴f′(x)=1-
,
∵函数f(x)=x+
(b∈R)的导函数在区间(1,2)上有零点,
∴当1-
=0时,b=x2,x∈(1,2)
∴b∈(1,4)
故选:D.
| b |
| x |
∴f′(x)=1-
| b |
| x2 |
∵函数f(x)=x+
| b |
| x |
∴当1-
| b |
| x2 |
∴b∈(1,4)
故选:D.
点评:本题考查了导数的运算法则和函零点存在定理,属于基础题

练习册系列答案
相关题目
现将周长为24cm的圆改为矩形 (周长不变),则该矩形面积大于32cm2的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
有2个人在一座7层大楼的底层进入电梯,假设每一个人自第二层开始在每一层离开电梯是等可能的,则这2个人在不同层离开的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
为了得到函数y=sin(2x+
)的图象,只需把函数y=sin2x图象上所有的点( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
函数y=sin(ωx+φ)的部分图象如图,则φ、ω可以取的一组值是( )
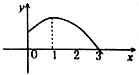

A、ω=
| ||||
B、ω=
| ||||
C、ω=
| ||||
D、ω=
|
已知函数f(x)满足3f(x)-f(
)=2x,则f(x)=( )
| 1 |
| x |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|