题目内容
已知(1-3x)2014=a0+a1x+a2x+…+a2014x2014,则
+
+…+
的值为( )
| a1 |
| 3 |
| a2 |
| 32 |
| a2014 |
| 32014 |
| A、3 | B、0 | C、-1 | D、-3 |
考点:二项式系数的性质
专题:二项式定理
分析:由题意可得a0=1,在所给的等式中,令x=
,可得1+
+
+…+
=0,由此求得
+
+…+
的值.
| 1 |
| 3 |
| a1 |
| 3 |
| a2 |
| 32 |
| a2014 |
| 32014 |
| a1 |
| 3 |
| a2 |
| 32 |
| a2014 |
| 32014 |
解答:
解:∵(1-3x)2014=a0+a1x+a2x+…+a2014x2014,∴a0=1,
令x=
,可得1+
+
+…+
=0,
∴
+
+…+
=-1,
故选:C.
令x=
| 1 |
| 3 |
| a1 |
| 3 |
| a2 |
| 32 |
| a2014 |
| 32014 |
∴
| a1 |
| 3 |
| a2 |
| 32 |
| a2014 |
| 32014 |
故选:C.
点评:本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于中档题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知两条直线a,b,两个平面α,β.给出下面四个命题:
①a∥b,a∥α⇒b∥α;
②a?α,b⊥β,α∥β⇒a⊥b;
③a⊥α,a∥b,b∥β⇒α∥β;
④α∥β,a∥b,a⊥α⇒b⊥β.
其中正确的命题序号为( )
①a∥b,a∥α⇒b∥α;
②a?α,b⊥β,α∥β⇒a⊥b;
③a⊥α,a∥b,b∥β⇒α∥β;
④α∥β,a∥b,a⊥α⇒b⊥β.
其中正确的命题序号为( )
| A、①② | B、②③ | C、①④ | D、②④ |
不等式|x|(1-x2)>0的解集是( )
| A、(-1,1) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
已知命题p:?φ∈R,使f(x)=sin(x+φ)为偶函数;命题q:?x∈R,cos2x+4sinx-3<0,则下列命题中为真命题的是( )
| A、p∧q |
| B、(¬p)∨q |
| C、p∨(¬q) |
| D、(¬p)∧(¬q) |
设等差数列{an}的前n项和为Sn,若S7>S8>S6,则满足Sn•Sn+1<0的正整数n的值为( )
| A、11 | B、12 | C、13 | D、14 |
在直角坐标系中,直线y=
x+2的倾斜角是( )
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
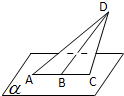 平面ACD⊥平面α,B为AC的中点,AC=2,∠CBD=60°,P是α内的动点,且P到直线BD的距离为
平面ACD⊥平面α,B为AC的中点,AC=2,∠CBD=60°,P是α内的动点,且P到直线BD的距离为