题目内容
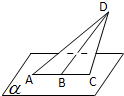平面ACD⊥平面α，B为AC的中点，AC=2，∠CBD=60°，P是α内的动点，且P到直线BD的距离为| 3 |
A、2
| ||||
B、
| ||||
| C、2 | ||||
D、
|
考点：点、线、面间的距离计算,三角形的面积公式
专题：空间位置关系与距离
分析：由题意判断P在平面α上的位置，然后求出△APC面积的最大值．
解答：
解：∵平面ACD⊥平面α，B为AC的中点，AC=2，∠CBD=60°，P是α内的动点，且P到直线BD的距离为
，
要求△APC面积的最大值，只需P到AC的距离的最大值，
显然当BP⊥AC时，P到AC的距离最大，如图
∴△APC面积的最大值：
×2×
=
．
故选：D．
解：∵平面ACD⊥平面α，B为AC的中点，AC=2，∠CBD=60°，P是α内的动点，且P到直线BD的距离为| 3 |
要求△APC面积的最大值，只需P到AC的距离的最大值，
显然当BP⊥AC时，P到AC的距离最大，如图
∴△APC面积的最大值：
| 1 |
| 2 |
| 3 |
| 3 |
故选：D．
点评：本题考查空间点、线、面距离的计算，考查空间想象能力．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
若{an}为等差数列，且a2+a5+a8=π，则tan（a3+a7）的值为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设A（2，1，3），B（0，1，0），则点A到点B距离为（ ）
| A、13 | ||
| B、12 | ||
C、
| ||
D、2
|
“函数f（x）=cos2ax-sin2ax的最小正周期为2π”是“a=-
”的（ ）
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在高台跳水运动中，运动员相对于水面的高度h（m）与起跳后的时间t（s）存在函数关系h（t）=-4.9t2+6.5t+10，则瞬时速度为0m/s的时刻是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|