题目内容
已知数列{an}满足an+1+an=4n-3(n∈N*),若对任意的n∈N*,都有an2+an+12≥20n-15成立,则a1的取值范围是 .
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:由an+1+an=4n-3(n∈N*),得an+2+an+1=4n+1,两式相减得出an+2-an=4.分n为奇数、n为偶数两种情况进行讨论,可分别求得an,an+1,进而可表示出不等式an2+an+12≥20n-15,分离出a1后化为最值可解.
解答:
解:∵an+1+an=4n-3(n∈N*),
∴an+2+an+1=4n+1,
两式相减得出an+2-an=4.
(1)当n为奇数时,令n=2k-1(k∈N*),
则有a2k+1-a2k-1=4.
∴an=a2k-1=a1+(k-1)×4=2n+a1-2.
又由已知an+1+an=4n-3,
∴an+1=2n-a1-1,
则an2+an+12≥20n-15,即为(2n+a1-2)2+(2n-a1-1)2≥20n-15,
整理可得a12-a1≥-4(n-2)2+6,
而-4(n-2)2+6≤6,
∴a12-a1≥6,解得a1≤-2或a1≥3①;
(2)当n为偶数时,令n=2k(k∈N*),则有a2k+2-a2k=4.
由a2+a1=1,得a2=1-a1,
∴an=a2k=a2+(k-1)×4=2n-a1-3.
由an+1+an=4n-3,得an+1=2n+a1,
则an2+an+12≥20n-15,即为(2n-a1-3)2+(2n+a1)2≥20n-15,
整理,得a12+3a1≥-4(n-2)2+4,
而-4(n-2)+4≤4,
∴a12+3a1≥4,解得a1≤-4或a1≥1②;
综上所述,联立①②,解得a1的取值范围是a1≤-4或a1≥3.
故答案为:a1≤-4或a1≥3.
∴an+2+an+1=4n+1,
两式相减得出an+2-an=4.
(1)当n为奇数时,令n=2k-1(k∈N*),
则有a2k+1-a2k-1=4.
∴an=a2k-1=a1+(k-1)×4=2n+a1-2.
又由已知an+1+an=4n-3,
∴an+1=2n-a1-1,
则an2+an+12≥20n-15,即为(2n+a1-2)2+(2n-a1-1)2≥20n-15,
整理可得a12-a1≥-4(n-2)2+6,
而-4(n-2)2+6≤6,
∴a12-a1≥6,解得a1≤-2或a1≥3①;
(2)当n为偶数时,令n=2k(k∈N*),则有a2k+2-a2k=4.
由a2+a1=1,得a2=1-a1,
∴an=a2k=a2+(k-1)×4=2n-a1-3.
由an+1+an=4n-3,得an+1=2n+a1,
则an2+an+12≥20n-15,即为(2n-a1-3)2+(2n+a1)2≥20n-15,
整理,得a12+3a1≥-4(n-2)2+4,
而-4(n-2)+4≤4,
∴a12+3a1≥4,解得a1≤-4或a1≥1②;
综上所述,联立①②,解得a1的取值范围是a1≤-4或a1≥3.
故答案为:a1≤-4或a1≥3.
点评:本题考查由数列递推式求数列通项、等差数列及不等式恒成立,考查分类与整合思想、转化思想.思维灵活性大,逻辑关系较复杂.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知动点P(x,y)满足
,动点Q(x,y)在曲线(x-1)2+y2=1上,则|PQ|的最大值与最小值的和为( )
|
A、
| ||||||
B、2
| ||||||
C、
| ||||||
D、3
|
已知全集U={1,2,3,4,5,6,7,8,9,10},集合A={2,3,5,9},集合B={4,5,6,7,9},则(∁UA)∩(∁UB)=( )
| A、{5,9} |
| B、{2,3} |
| C、{1,8,10} |
| D、{4,6,7} |
设函数f(x)的定义域为D,若存在非零实数t使得对于任意x∈M(M⊆D),有x+t∈D,且f(x+t)≥f(x),则称f(x)为M上的“t高调函数”.如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且f(x)为R上的“4高调函数”,那么实数a的取值范围是( )
A、[-
| ||||||||
| B、[-1,1] | ||||||||
C、[-1,
| ||||||||
D、[-
|
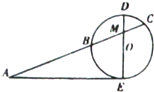 如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=
如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=