Question

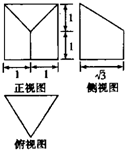
已知一个几何体的三视图如图所示，则该几何体的体积为

 

．

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由已知中的三视图，可得该几何体是由一个三棱柱，挖去一个三棱锥，所得的组合体，进而可得答案．

解答： 解：由已知中的三视图，可得该几何体是：
一个三棱柱挖掉一个三棱锥，所得的组合体，
其直观图如下图所示：

∵三棱柱的体积V=

3

4

×22×2=2

3

，
挖去的棱锥体积V=

1

3

×(

3

4

×22)×1=

3

3

，
故该几何体的体积为2

3

-

3

3

=

5 3

3

，
故答案为：

5 3

3

点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状是解答的关键．