题目内容
已知动点P(x,y)满足
,动点Q(x,y)在曲线(x-1)2+y2=1上,则|PQ|的最大值与最小值的和为( )
|
A、
| ||||||
B、2
| ||||||
C、
| ||||||
D、3
|
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:作出不等式度对应的平面区域,利用点和圆的位置关系即可得到结论.
解答:
解:作出不等式组对应的平面区域如图: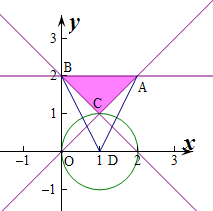
则B(0,2),A(2,2),C(1,1),
∵点C(1,1)也在圆上,
∴当P,Q同时在C处,|PQ|的距离最小为0,
根据对称性可知,|AD|=|BD|,即A,B到圆心D的距离相等,
∴当P位于B或A,Q位于过BD或AD延长线与圆相交的位置,此时|PQ|最大,
∵|BD|=
=
,半径r=1,
∴|PQ|最大值为
+1,
即|PQ|的最大值与最小值的和为
+1,
故选:A

则B(0,2),A(2,2),C(1,1),
∵点C(1,1)也在圆上,
∴当P,Q同时在C处,|PQ|的距离最小为0,
根据对称性可知,|AD|=|BD|,即A,B到圆心D的距离相等,
∴当P位于B或A,Q位于过BD或AD延长线与圆相交的位置,此时|PQ|最大,
∵|BD|=
| 12+22 |
| 5 |
∴|PQ|最大值为
| 5 |
即|PQ|的最大值与最小值的和为
| 5 |
故选:A
点评:本题主要考查线性规划的应用,利用数形结合,以及点与圆的位置关系,结合距离公式是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设i为虚数单位,则复数z=
在复平面内对应的点位于( )
| i3 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知弹簧的一端固定在地面上,另一端固定一个小球,已知小球在达到平衡位置之前处于加速状态,且加速度与时间的函数关系为a(t)=2t+
+3,则当t=1时小球的速度为( )
| 10 |
| 1+t |
| A、4+10ln2 |
| B、5+10ln2 |
| C、4-10ln2 |
| D、5-10ln2 |
已知x,y满足不等式组
,则目标函数z=2x+y的最大值为( )
|
| A、5 | B、6 | C、7 | D、8 |
设m∈R,则m=1是直线l1:(m+1)x+2y-1=0和l2:x+my+4=0平行的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分又不必要条件 |