题目内容
如图，PQ是半径为1的圆A的直径，△ABC是边长为1的正三角形，则| BP |
| CQ |
（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的三角形法则、向量的数量积运算及三角函数的值域即可得出．
解答：
解：根据三角形法则：
=
-
，
=
-
所以：
•
=(
-
)•(
-
)=-1-
•
=-1-
•
-
•
+
设：∠BAP=θ
则：
•
=-cos(θ+60°)-cos(180°-θ)-
=sin（θ+30°）-
当θ=60°时，
•
的最大值为：
故选：B
| BP |
| AP |
| AB |
| CQ |
| AQ |
| AC |
所以：
| BP |
| CQ |
| AP |
| AB |
| AQ |
| AC |
| AP |
| AC |
| AP |
| AC |
| AQ |
| AB |
| 1 |
| 2 |
设：∠BAP=θ
则：
| BP |
| CQ |
| 1 |
| 2 |
=sin（θ+30°）-
| 1 |
| 2 |
当θ=60°时，
| BP |
| CQ |
| 1 |
| 2 |
故选：B
点评：本题考查的知识要点：利用三角形法则求向量的加减，向量的数量积，两角和与差的正弦公式，及三角函数的单调性．属于基础题．
练习册系列答案
相关题目
若sinα＞0，tanα＜0，则角α是第（ ）象限角．
| A、一 | B、二 | C、三 | D、四 |
设集合A={x|x2-3x-4＞0}，B={x|-2≤x≤3}，则（∁RA）∩B=（ ）
| A、R |
| B、[-2，-1] |
| C、[-1，3] |
| D、[-2，4] |
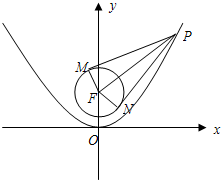已知抛物线C：x2=2py（p＞0）的焦点为F，点A（a，4）为抛物线C上的定点，点P为抛物线C上的动点．且△FOA的外接圆圆心到准线的距离为