题目内容
已知
=(2,-1,2),
=(-1,3,-3),
=(13,6,λ),若向量
,
,
共面,则λ= .
| a |
| b |
| c |
| a |
| b |
| c |
考点:共线向量与共面向量
专题:平面向量及应用
分析:由于向量
,
,
共面,利用向量共面定理可得:存在唯一一对实数m,n使得
=m
+n
,解出即可.
| a |
| b |
| c |
| c |
| a |
| b |
解答:
解:∵向量
,
,
共面,
∴存在唯一一对实数m,n使得
=m
+n
,
∴
,解得
.
故答案为:3.
| a |
| b |
| c |
∴存在唯一一对实数m,n使得
| c |
| a |
| b |
∴
|
|
故答案为:3.
点评:本题考查了向量共面定理,属于基础题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
在从2011年到2014年期间,甲每年1月1日都到银行存入a元的一年定期储蓄.若年利率为q保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
| A、a(1+q)4 | ||
| B、a(1+q)5 | ||
C、
| ||
D、
|
 已知f(x)=6cos2
已知f(x)=6cos2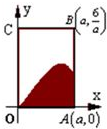 如图,矩形OABC内阴影部分是由曲线f(x)=sinx(x∈(0,π)及直线x=a(a∈(0,π)与x轴围成,向矩形OABC内随机的投掷一点,若落在阴影部分的概率为
如图,矩形OABC内阴影部分是由曲线f(x)=sinx(x∈(0,π)及直线x=a(a∈(0,π)与x轴围成,向矩形OABC内随机的投掷一点,若落在阴影部分的概率为