题目内容
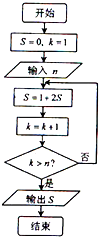 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )| A、3 | B、4 | C、5 | D、6 |
考点:程序框图
专题:算法和程序框图
分析:框图在输入n的值后,根据对S和k的赋值执行运算,S=1+2S,k=k+1,然后判断k时否大于n,不满足继续执行循环,满足跳出循环,由题意,说明当算出的值S∈(30,40)后进行判断时判断框中的条件满足,即可求出此时的n值.
解答:
解:框图首先给累加变量S赋值0,给循环变量k赋值1,
输入n的值后,执行S=1+2×0=1,k=1+1=2;
判断2>n不成立,执行S=1+2×1=3,k=2+1=3;
判断3>n不成立,执行S=1+2×3=7,k=3+1=4;
判断4>n不成立,执行S=1+2×7=15,k=4+1=5.
判断5>n不成立,执行S=1+2×15=31,k=5+1=6.
此时S=31∈(30,40),是输出的值,说明下一步执行判断时判断框中的条件应该满足,
即6>n满足,所以正整数n的值应为5.
故选C.
输入n的值后,执行S=1+2×0=1,k=1+1=2;
判断2>n不成立,执行S=1+2×1=3,k=2+1=3;
判断3>n不成立,执行S=1+2×3=7,k=3+1=4;
判断4>n不成立,执行S=1+2×7=15,k=4+1=5.
判断5>n不成立,执行S=1+2×15=31,k=5+1=6.
此时S=31∈(30,40),是输出的值,说明下一步执行判断时判断框中的条件应该满足,
即6>n满足,所以正整数n的值应为5.
故选C.
点评:本题考查了程序框图中的循环结构,是直到型循环,即先执行后判断,不满足条件执行循环,直到条件满足跳出循环,算法结束,是基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知函数y=Asin(ωx+φ)在同一周期内,当x=
时,取得最大值y=3,当x=
时,取得最小值y=-3,则函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=3sin(2x-
| ||||
B、y=3sin(
| ||||
C、y=3sin(2x+
| ||||
D、y=3sin(2x+
|
由曲线y=
,直线y=4x,x=1及x轴共同围成的封闭图形的面积为( )
| 1 |
| x |
A、ln2-
| ||
B、
| ||
C、ln2+
| ||
| D、1+ln2 |
在△ABC中,A=60°,b=1,c=4,则△ABC外接圆的直径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+a3(1+x)3+a4(1+x)4+a5(1+x)5,其中a0,a1,a2,a3,a4,a5为实数,则a3=( )
| A、-10 | B、10 |
| C、20 | D、-20 |
过椭圆
+
=1(a>b>0)左焦点F1作垂直于x轴的直线交椭圆于AB两点,若△ABF2为等边三角形,则该椭圆离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
