题目内容
已知sin（π-α）=-
，π＜α＜
，则tanα=（ ）
| 12 |
| 13 |
| 3π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点：同角三角函数基本关系的运用,运用诱导公式化简求值
专题：三角函数的求值
分析：已知等式左边利用诱导公式化简，求出sinα的值，根据α的范围，利用同角三角函数间基本关系求出cosα的值，即可确定出tanα的值．
解答：
解：∵sin（π-α）=sinα=-
，π＜α＜
，
∴cosα=-
=-
，
则tanα=
=
．
故选：C．
| 12 |
| 13 |
| 3π |
| 2 |
∴cosα=-
| 1-sin2α |
| 5 |
| 13 |
则tanα=
| sinα |
| cosα |
| 12 |
| 5 |
故选：C．
点评：此题考查了同角三角函数基本关系的运用，以及运用诱导公式化简求值，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
在如图图形中，小黑点的个数构成一个数列{an}的前3项．已知函数y=Asin（ωx+φ）在同一周期内，当x=
时，取得最大值y=3，当x=
时，取得最小值y=-3，则函数的解析式为（ ）
| π |
| 12 |
| 7π |
| 12 |
A、y=3sin（2x-
| ||||
B、y=3sin（
| ||||
C、y=3sin（2x+
| ||||
D、y=3sin（2x+
|
在△ABC中，A=60°，b=1，c=4，则△ABC外接圆的直径为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
若将函数f（x）=x5表示为f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4+a5（1+x）5，其中a0，a1，a2，a3，a4，a5为实数，则a3=（ ）
| A、-10 | B、10 |
| C、20 | D、-20 |
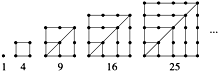我们把1，4，9，16，25，…这些数称做正方形数，这是因为这些数目的点子可以排成一个正方形（如图）．试求第n个正方形数是（ ）| A、n（n-1） |
| B、n（n+1） |
| C、n2 |
| D、（n+1）2 |
过椭圆
+
=1（a＞b＞0）左焦点F1作垂直于x轴的直线交椭圆于AB两点，若△ABF2为等边三角形，则该椭圆离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（1+x）2n+1的展开式中，二项式系数最大的项所在的项数是（ ）
| A、n，n+1 |
| B、n-1，n |
| C、n+1，n+2 |
| D、n+2，n+3 |