题目内容
函数f(x)=ax2+bx+c(a≠0)的图象关于直线x=-
对称.据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+nf(x)+g=0的解集不可能是( )
| b |
| 2a |
| A、{1,3} |
| B、{2,4} |
| C、{1,2,3,4} |
| D、{1,2,4,8} |
考点:二次函数的性质
专题:函数的性质及应用
分析:直接利用函数的对称性看能否找到对称轴,当是四个数时看能否使得其中两个的和等于另外两个的和,答案易求得.
解答:
解:f(x)=ax2+bx+c的对称轴为直线x=-
令设方程m[f(x)]2+nf(x)+g=0的解为f1(x),f2(x)
则必有f1(x)=y1=ax2+bx+c,f2(x)=y2=ax2+bx+c
那么从图象上看,y=y1,y=y2是一条平行于x轴的直线
它们与f(x)有交点
由于对称性,则方程y1=ax2+bx+c的两个解x1,x2要关于直线x=-
对称
也就是说x1+x2=-
同理方程y2=ax2+bx+c的两个解x3,x4也要关于直线x=-
对称
那就得到x3+x4=-
,
在A中,可以找到对称轴直线x=2,
在B中,可以找到对称轴直线X=3,
在C中,可以找到对称轴直线X=2.5,
也就是1,4为一个方程的解,2,3为一个方程的解
所以得到的解的集合可以是{1,2,3,4}
而在D中,{1,2,4,8}
找不到这样的组合使得对称轴一致,
也就是说无论怎么分组,
都没办法使得其中两个的和等于另外两个的和
故答案D不可能
故选D.
| b |
| 2a |
令设方程m[f(x)]2+nf(x)+g=0的解为f1(x),f2(x)
则必有f1(x)=y1=ax2+bx+c,f2(x)=y2=ax2+bx+c
那么从图象上看,y=y1,y=y2是一条平行于x轴的直线
它们与f(x)有交点
由于对称性,则方程y1=ax2+bx+c的两个解x1,x2要关于直线x=-
| b |
| 2a |
也就是说x1+x2=-
| b |
| a |
同理方程y2=ax2+bx+c的两个解x3,x4也要关于直线x=-
| b |
| 2a |
那就得到x3+x4=-
| b |
| a |
在A中,可以找到对称轴直线x=2,
在B中,可以找到对称轴直线X=3,
在C中,可以找到对称轴直线X=2.5,
也就是1,4为一个方程的解,2,3为一个方程的解
所以得到的解的集合可以是{1,2,3,4}
而在D中,{1,2,4,8}
找不到这样的组合使得对称轴一致,
也就是说无论怎么分组,
都没办法使得其中两个的和等于另外两个的和
故答案D不可能
故选D.
点评:本题考查了函数的对称性问题,解决函数问题可结合图象,利用数形结合来解答.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
若△ABC的内角A,B,C满足
=
=
,则cosB=( )
| 2 |
| sinA |
| 3 |
| sinB |
| 4 |
| sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知等差数列{an}的前n项和为Sn,若S10=
(6x+
)dx,则a3+a8=( )
| ∫ | 2 0 |
| 3 |
| 2 |
| A、3 | B、6 | C、9 | D、12 |
如图,在复平面内,复数z1,z2对应的向量分别是
,
,则|z1+z2|=( )

| OA |
| OB |

| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
执行如图的程序框图,输出的结果是( )
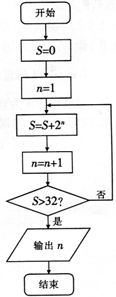

| A、3 | B、4 | C、5 | D、6 |
已知在二项式(
-
)n的展开式中,仅有第9项的二项式系数最大,则展开式中,有理项的项数是( )
| 3 | x |
| 2 | ||
|
| A、1 | B、2 | C、3 | D、4 |
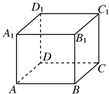 如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量
如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量| AC1 |
①(
| AB |
| BC |
| CC1 |
②(
| AA1 |
| A1D1 |
| D1C1 |
③(
| AB |
| BB1 |
| B1C1 |
④(
| AA1 |
| A1B1 |
| B1C1 |
| A、①③ | B、②④ |
| C、③④ | D、①②③④ |
函数f(x)=x-sinx是( )
| A、奇函数且单调递增 |
| B、奇函数且单调递减 |
| C、偶函数且单调递增 |
| D、偶函数且单调递减 |
 如图,AB是圆O的直径,AB=2,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若DA=DC,则∠BDC=
如图,AB是圆O的直径,AB=2,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若DA=DC,则∠BDC=