题目内容
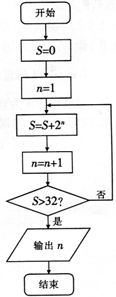
执行如图的程序框图，输出的结果是（ ）
| A、3 | B、4 | C、5 | D、6 |
考点：程序框图
专题：算法和程序框图
分析：算法的功能是求满足S=2+22+…+2n＞32的最小的正整数n+1的值，利用等比数列的前n项和公式求得满足S＞32的最小的n值，可得输出的n值．
解答：
解：由程序框图知：算法的功能是求满足S=2+22+…+2n＞32的最小的正整数n+1的值，
∵S=2+22+…+2n=
=2n+1-2＞32⇒n＞4，
∴输出的n=5+1=6．
故选：D．
∵S=2+22+…+2n=
| 2(1-2n) |
| 1-2 |
∴输出的n=5+1=6．
故选：D．
点评：本题考查了循环结构的程序框图，根据框图的流程判断算法的功能及确定输出的n值是解答本题的关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
某程序框图如图所示，若a=3，则该程序运行后，输出的x的值为（ ）
| A、33 | B、31 | C、29 | D、27 |
设变量x，y满足约束条件
，其中k＞0．若
的最大值为1，则实数k的取值范围是（ ）
|
| y |
| x |
| A、（1，+∞） |
| B、[1，+∞） |
| C、（0，1] |
| D、（0，1） |
函数f（x）=ax2+bx+c（a≠0）的图象关于直线x=-
对称．据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f（x）]2+nf（x）+g=0的解集不可能是（ ）
| b |
| 2a |
| A、{1，3} |
| B、{2，4} |
| C、{1，2，3，4} |
| D、{1，2，4，8} |
框图中错误的是（ ）
| A、k未赋值 |
| B、循环结构有错 |
| C、s的计算不对 |
| D、判断条件不成立 |
按如图程序框图运算：若x=4，则运算进行几次才停止？（ ）
| A、3 | B、4 | C、5 | D、6 |