题目内容
已知在△ABC中，cosA=
，a=4，b=3，求角C．
| 3 |
| 5 |
考点：余弦定理
专题：三角函数的求值,解三角形
分析：利用余弦定理列出关系式，将cosA，a，b的值代入求出c的值，利用余弦定理求出cosC的值，即可确定出C的度数．
解答：
解：∵在△ABC中，cosA=
，a=4，b=3，
∴由余弦定理得a2=b2+c2-2bccosA，即16=9+c2-6×
c，
整理得：5c2-18c-35=0，
解得：c=5或c=-
（舍），
∴由余弦定理得cosC=
=
=0，
∵0＜C＜180°，
∴C=90°．
| 3 |
| 5 |
∴由余弦定理得a2=b2+c2-2bccosA，即16=9+c2-6×
| 3 |
| 5 |
整理得：5c2-18c-35=0，
解得：c=5或c=-
| 7 |
| 5 |
∴由余弦定理得cosC=
| a2+b2-c2 |
| 2ab |
| 16+9-25 |
| 2×4×3 |
∵0＜C＜180°，
∴C=90°．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
10名工人某天生产同一零件，生产的件数是15，17，14，10，15，17，17，16，14，12，设其众数为a，中位数为b，平均数为c，则有（ ）
| A、c＞a＞b |
| B、a＞b＞c |
| C、b＞c＞a |
| D、c＞b＞a |
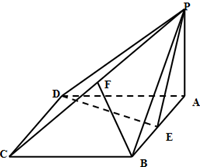如图，四棱锥P-ABCD的底面ABCD是菱形，∠BCD=60°，PA⊥面ABCD，E是AB的中点，F是PC的中点．
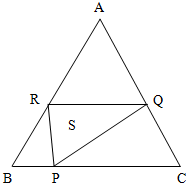如图，在正△ABC的边BC、CA、AB上分别取点P、Q、R，使CQ=2BP，AR=3BP．已知正三角形的边长是11cm，BP=xcm，△PQR的面积为S