题目内容
求函数y=
(1≤x≤2)的值域.
| x2 |
| x-3 |
考点:函数的值域
专题:计算题,函数的性质及应用
分析:求导判断函数的单调性,由单调性求值域.
解答:
解:∵y′=
=
,
又∵1≤x≤2,
∴y′<0,
则y=
在[1,2]上单调递减,
则
≤
≤
,
即-4≤y≤-
.
则函数y=
(1≤x≤2)的值域为[-4,-
].
| 2x(x-3)-x2 |
| (x-3)2 |
| x(x-6) |
| (x-3)2 |
又∵1≤x≤2,
∴y′<0,
则y=
| x2 |
| x-3 |
则
| 22 |
| 2-3 |
| x2 |
| x-3 |
| 12 |
| 1-3 |
即-4≤y≤-
| 1 |
| 2 |
则函数y=
| x2 |
| x-3 |
| 1 |
| 2 |
点评:本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
相关题目
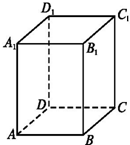 如图,已知长方体ABCD-A1B1C1D1中,AB=
如图,已知长方体ABCD-A1B1C1D1中,AB= 如图,PA与⊙O相切于点A,D为PA的中点,过点D引割线交⊙O于B,C两点,若∠DCP=25°,则∠DPB=
如图,PA与⊙O相切于点A,D为PA的中点,过点D引割线交⊙O于B,C两点,若∠DCP=25°,则∠DPB=