题目内容
11．若母线长是$2\sqrt{2}$cm的圆锥的轴截面的面积是4cm2，则此圆锥的高是2cm．分析 设圆锥的高为h，则底面半径为$\sqrt{8-{h}^{2}}$，利用圆锥的轴截面的面积是4cm2，得$\frac{1}{2}×2\sqrt{8-{h}^{2}}×h$=4，即可得出结论．
解答 解：设圆锥的高为h，则底面半径为$\sqrt{8-{h}^{2}}$，
∵圆锥的轴截面的面积是4cm2，
∴$\frac{1}{2}×2\sqrt{8-{h}^{2}}×h$=4，
∴h=2cm，
故答案为：2cm．
点评 本题考查圆锥的轴截面的面积的计算，考查方程思想，比较基础．
练习册系列答案
相关题目
4．在△ABC中，内角A，B，C的对边分别是a，b，c，若bcosC=（2a-c）cosB，则B=（ ）
| A． | 30° | B． | 60° | C． | 120° | D． | 150° |
19．一组数据3，4，5，s，t的平均数是4，这组数据的中位数是m，对于任意实数s，t，从3，4，5，s，t，m这组数据中任取一个，取到数字4的概率的最大值为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{5}$ |
6．已知函数f（x）=sin（2x+φ），其中φ为实数，若f（x）≤|f（$\frac{π}{6}$）|对x∈R恒成立，且f（$\frac{π}{2}$）＞f（π），则f（x）的单调递增区间是（ ）
| A． | [kπ-$\frac{π}{3}$，kπ+$\frac{π}{6}$]（k∈Z） | B． | [kπ，kπ+$\frac{π}{2}$]（k∈Z） | C． | [kπ-$\frac{π}{6}$，kπ+$\frac{2π}{3}$]（k∈Z） | D． | [kπ-$\frac{π}{2}$，kπ]（k∈Z） |
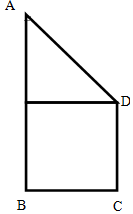已知四边形ABCD为直角梯形，AB∥CD，AB=4，BC=CD=2，AB⊥BC，现将该梯形绕AB所在直线旋转一周，得到一个封闭的几何体，求该几何体的表面积及体积．