题目内容
3.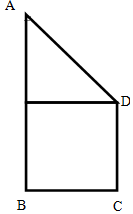 已知四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB所在直线旋转一周,得到一个封闭的几何体,求该几何体的表面积及体积.
已知四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB所在直线旋转一周,得到一个封闭的几何体,求该几何体的表面积及体积.
分析 通过已知条件知道,绕AB旋转一周形成的封闭几何体是上面是圆锥,下面是圆柱的图形.所以该几何体的表面积便是圆锥、圆柱的表面积和底面圆的面积的和,该几何体的体积便是圆锥、圆柱体积的和,所以根据已知的边的长度及圆锥、圆柱的表面积公式,及体积公式即可求出该几何体的表面积和体积.
解答 解:依题旋转后形成的几何体为上部为圆锥,下部为圆柱的图形,如下图所示:
其表面积S=圆锥侧面积+圆柱侧面积+圆柱底面积;
∴S=4$\sqrt{2}$π+8π+4π=12π+4$\sqrt{2}$π;
其体积V=圆锥体积+圆柱体积;
∴V=$\frac{8}{3}$π+8π=$\frac{32}{3}$π.
点评 考查对由平面图形绕一直线旋转之后形成的立体图形的判断,以及圆锥、圆柱的表面积公式,体积公式.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
18.下列说法正确的是( )
| A. | 函数的极大值就是函数的最大值 | |
| B. | 函数的极小值就是函数的最小值 | |
| C. | 函数的最值一定是极值 | |
| D. | 闭区间上的连续函数一定存在最大值与最小值 |
8.已知等边三角形ABC的边长为1,若$\overrightarrow{BC}=4\overrightarrow{BE},\overrightarrow{AD}=\overrightarrow{DC}$,则$\overrightarrow{BD}•\overrightarrow{AE}$的值为( )
| A. | -2 | B. | $-\frac{9}{16}$ | C. | $\frac{9}{16}$ | D. | 2 |