题目内容
19.函数$y=3\sqrt{2x-1}+4\sqrt{5-2x}$的最大值为10.分析 先求出x的范围,再根据柯西不等式即可求出答案.
解答 解:由$y=3\sqrt{2x-1}+4\sqrt{5-2x}$,可得$\left\{\begin{array}{l}{2x-1≥0}\\{5-2x≥0}\end{array}\right.$,解得$\frac{1}{2}$≤x≤$\frac{5}{2}$,
$y=3\sqrt{2x-1}+4\sqrt{5-2x}$≤$\sqrt{{3}^{2}+{4}^{2}}$•$\sqrt{(\sqrt{2x-1})^{2}+(\sqrt{5-2x})^{2}}$=5$\sqrt{2x-1+5-2x}$=10,
当且仅当3$\sqrt{5-2x}$=4$\sqrt{2x-1}$,即x=$\frac{61}{50}$时取等号,
故函数$y=3\sqrt{2x-1}+4\sqrt{5-2x}$的最大值为10,
故答案为:10
点评 本题考查二元柯西不等式及应用,考查基本的运算能力,是一道基础题.

练习册系列答案
相关题目
15.已知正方体的外接球的体积为$\frac{32}{3}π$,则该正方体的表面积为( )
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{64}{3}$ | D. | 32 |
4.函数f(x)=-4x3+3x+2(x∈[0,1])的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
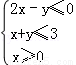 ,则目标函数z=2x+y的最大值为( )
,则目标函数z=2x+y的最大值为( )