题目内容
4.在△ABC中,内角A,B,C的对边分别是a,b,c,若bcosC=(2a-c)cosB,则B=( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 利用正弦定理化简可得:sinBcosC=2sinAcosB-sinCcosB,根据和与差的公式,可得sinA=2sinAcosB,即可求解B的值.
解答 解:由题意,bcosC=(2a-c)cosB,
由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB
得:sinBcosC+sinCcosB=2sinAcosB.
即sinA=2sinAcosB
∵0<A<π,sinA≠0,
∴cosB=$\frac{1}{2}$
∵0<B<π,
∴B=$\frac{π}{3}$.
故选B
点评 本题考查了正弦定理和和与差的公式的灵活运用.属于基础题.

练习册系列答案
相关题目
15.现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
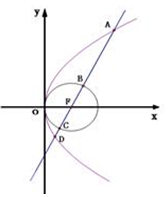 圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点
圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点