题目内容
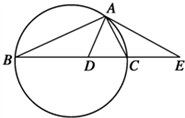如图，设△ABC的外接圆的切线AE与BC的延长线交于点E，∠BAC的平分线与BC交于点D．求证：
（1）∠ADE=∠DAC
（2）ED2=EC•EB．
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（1）由弦切角定理，结合三角形的外角证出∠ADE=∠DAE；
（2）由（1）得EA=ED，再由切割线定理，得EA2=EC•EB，结合EA=ED，即可证出ED2=EC•EB．
（2）由（1）得EA=ED，再由切割线定理，得EA2=EC•EB，结合EA=ED，即可证出ED2=EC•EB．
解答：
证明：（1）∵AE是圆的切线，∴∠ABC=∠CAE．
∵AD是∠BAC的平分线，∴∠BAD=∠CAD，
从而∠ABC+∠BAD=∠CAE+∠CAD．
∵∠ADE=∠ABC+∠BAD，∠DAE=∠CAD+∠CAE，
∴∠ADE=∠DAE；
（2）由（1）得EA=ED．
∵AE是圆的切线，∴由切割线定理，得EA2=EC•EB．
结合EA=ED，得ED2=EC•EB．
∵AD是∠BAC的平分线，∴∠BAD=∠CAD，
从而∠ABC+∠BAD=∠CAE+∠CAD．
∵∠ADE=∠ABC+∠BAD，∠DAE=∠CAD+∠CAE，
∴∠ADE=∠DAE；
（2）由（1）得EA=ED．
∵AE是圆的切线，∴由切割线定理，得EA2=EC•EB．
结合EA=ED，得ED2=EC•EB．
点评：熟练掌握三角形的外角定理、角平分线的性质、切割线定理等是解题的关键．
练习册系列答案
相关题目
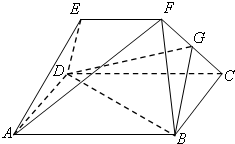如图几何体中，四边形ABCD为矩形，AB=2BC=4，BF=CF=AE=DE，EF=2，EF∥AB，AF⊥CF．
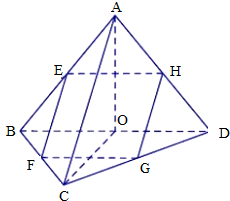在三棱锥A-BCD中，点E、F、G、H分别是AB、BC、CD、DA的中点．