题目内容
已知极坐标系的极点在直角坐标系的原点O处,极轴与x轴的正半轴重合,直线l的参数方程为
(t为参数,0≤α<π),圆C的极坐标方程为ρ2-8ρcosθ+12=0.若tanα=
,直线l与圆C交于A、B两点,求|OA|+|OB|的值.
|
| 1 |
| 2 |
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:选作题,坐标系和参数方程
分析:把圆C的极坐标方程化为直角坐标方程,把直线l的参数方程代入圆的方程,由韦达定理可得t1+t2=|OA|+|OB|=8cosα.再由条件求得cosα的值,可得|OA|+|OB|的值.
解答:
解:圆C的极坐标方程为ρ2-8ρcosθ+12=0,化为直角坐标方程为x2+y2-8x+12=0即(x-4)2+y2=4,
表示以(4,0)为圆心、半径等于2的圆.
把直线l的参数方程
代入圆的方程,可得 t2-8cosαt+12=0.
由韦达定理可得t1•t2=12>0,t1+t2=|OA|+|OB|=8cosα.
再由直线l的倾斜角为α,且tanα=
,可得cosα=
,∴|OA|+|OB|=8×
=
.
表示以(4,0)为圆心、半径等于2的圆.
把直线l的参数方程
|
由韦达定理可得t1•t2=12>0,t1+t2=|OA|+|OB|=8cosα.
再由直线l的倾斜角为α,且tanα=
| 1 |
| 2 |
2
| ||
| 5 |
2
| ||
| 5 |
16
| ||
| 5 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,参数的几何意义,韦达定理的应用,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
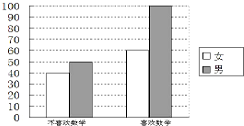 为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.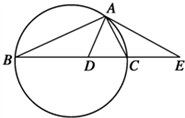 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与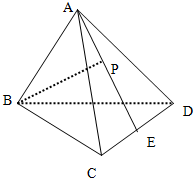 已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.
已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.