题目内容
已知命题P:
+
=1表示焦点在y轴上的椭圆,命题Q:双曲线
-
=1的离心率e∈(
,
),若命题P、Q中有且只有一个为真命题,求实数m的取值范围.
| x2 |
| 2m |
| y2 |
| 9-m |
| y2 |
| 5 |
| x2 |
| m |
| ||
| 2 |
| 2 |
考点:复合命题的真假
专题:圆锥曲线的定义、性质与方程
分析:利用椭圆与双曲线的性质可得命题P,Q中的m的取值范围,又命题P、Q中有且只有一个为真命题,则P,Q必一真一假.求出即可.
解答:
解:若P真,则有9-m>2m>0,即0<m<3.
若Q真,则有
,解得
<m<5.
因命题P、Q中有且只有一个为真命题,则P、Q一真一假.
①若P真,Q假,则
,解得0<m≤
;
②若P假,Q真,则
,解得3≤m<5;
综上,m的范围为(0,
)∪[3,5).
若Q真,则有
|
| 5 |
| 2 |
因命题P、Q中有且只有一个为真命题,则P、Q一真一假.
①若P真,Q假,则
|
| 5 |
| 2 |
②若P假,Q真,则
|
综上,m的范围为(0,
| 5 |
| 2 |
点评:本题考查了椭圆双曲线的性质、命题的真假判断方法,考查了推理能力,属于中档题.

练习册系列答案
相关题目
 某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).
某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).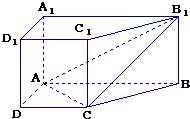 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.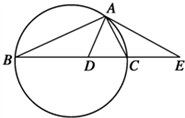 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点,M为BC的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点,M为BC的中点.