题目内容
若数列{an}满足a1=2,an+1=
(n∈N*),则该数列的前2014项的乘积a1•a2•a3…a2013•a2014=( )
| 1+an |
| 1-an |
| A、3 | B、-6 | C、2 | D、1 |
考点:数列递推式
专题:等差数列与等比数列
分析:由递推公式推导出{an}是周期为4的周期数列,且a1•a2•a3•a4=1,由此能求出结果.
解答:
解:∵数列{an}满足a1=2,an+1=
(n∈N*),
∴a2=
=-3,
a3=
=-
,
a4=
=
,
a5=
=2,
∴{an}是周期为4的周期数列,
且a1•a2•a3•a4=1,
∵2014=503×4+2,
∴a1•a2•a3…a2013•a2014=1503×2×(-3)=-6.
故选:B.
| 1+an |
| 1-an |
∴a2=
| 1+2 |
| 1-2 |
a3=
| 1-3 |
| 1+3 |
| 1 |
| 2 |
a4=
1-
| ||
1+
|
| 1 |
| 3 |
a5=
1+
| ||
1-
|
∴{an}是周期为4的周期数列,
且a1•a2•a3•a4=1,
∵2014=503×4+2,
∴a1•a2•a3…a2013•a2014=1503×2×(-3)=-6.
故选:B.
点评:本题考查数列的前2014项积的求法,解题时要认真审题,注意数列的周期性的合理运用.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
某学生在高三下期最近五次考试中的数学成绩如下表:
设回归直线方程
=bx+a,则点(a,b)在直线x+3y-20=0的( )
| 第x次考试 | 1 | 2 | 3 | 4 | 5 |
| 数学成绩y分 | 125 | 132 | 137 | 126 | 130 |
 |
| y |
| A、左上方 | B、左下方 |
| C、右上方 | D、右下方 |
当0≤x≤
时,|ax-2x3|≤
恒成立,则实数a的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、a≥-
| ||||
D、a≤
|
已知等边三角形ABC的边长为1,则
•
=( )
| AB |
| BC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设i为虚数单位,则复数z=
在复平面对应的点位于( )
| 1-2i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
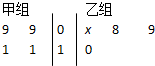 如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )
如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )