题目内容
某学生在高三下期最近五次考试中的数学成绩如下表：
设回归直线方程
=bx+a，则点（a，b）在直线x+3y-20=0的（ ）
| 第x次考试 | 1 | 2 | 3 | 4 | 5 |
| 数学成绩y分 | 125 | 132 | 137 | 126 | 130 |
 |
| y |
| A、左上方 | B、左下方 |
| C、右上方 | D、右下方 |
考点：线性回归方程
专题：计算题,概率与统计
分析：根据所给的数据先做出数据的平均数，即样本中心点，根据最小二乘法做出线性回归方程的系数，即可得出结论．
解答：
解：由题意，
=3，
=130，
xi2=55，
xiyi=1954，
∴b=
=0.4，
∴a=130-0.4×3=128.8，
点（128.8，0.4）代入直线x+3y-20=0＞0，
∴点（128.8，0.4）在直线x+3y-20=0的右上方．
故选：C．
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
|
| i=1 |
∴b=
| 1954-5•3•130 |
| 55-5•9 |
∴a=130-0.4×3=128.8，
点（128.8，0.4）代入直线x+3y-20=0＞0，
∴点（128.8，0.4）在直线x+3y-20=0的右上方．
故选：C．
点评：本题主要考查了线性回归方程等知识，考查了学生的数据处理能力和应用意识．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
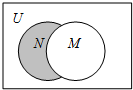
设全集U={1，2，3，4，5}，M={3，4}，N={2，3}，则图中阴影部分所表示的集合是（ ）
| A、{1，2，4} |
| B、{2，4} |
| C、{2} |
| D、{1，2，5} |
袋中共有6个除了颜色外完全相同的球，其中有1个红球，2个白球和3个黑球，从袋中任取1球，则取出的球为恰好是黑球的概率等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知{an}为等差数列，且a4+a8=12，S9=45，则S10的值为（ ）
| A、110 | B、60 | C、55 | D、50 |