题目内容
已知直线x-y=0与抛物线x2=2py交于A、B两点,若点P(2,2)为AB中点,求抛物线方程.
考点:抛物线的简单性质,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2).由于
=2py1,
=2py2,可得(x1+x2)(x1-x2)=2p(y1-y2).再利用斜率计算公式与中点坐标公式即可得出.
| x | 2 1 |
| x | 2 2 |
解答:
解:设A(x1,y1),B(x2,y2).
∵
=2py1,
=2py2,
∴(x1+x2)(x1-x2)=2p(y1-y2).
又
=1,x1+x2=2×2,
∴4=2p,解得p=2.
∴抛物线的方程为:x2=4y.
∵
| x | 2 1 |
| x | 2 2 |
∴(x1+x2)(x1-x2)=2p(y1-y2).
又
| y1-y2 |
| x1-x2 |
∴4=2p,解得p=2.
∴抛物线的方程为:x2=4y.
点评:本题考查了“点差法”、斜率计算公式与中点坐标公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=
+lg(3x+1)的定义域为( )
| 2x2 | ||
|
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-∞,
|
若正数a,b,c成公差不为零的等差数列,则( )
| A、lga,lgb,lgc成等差数列 |
| B、lga,lgb,lgc成等比数列 |
| C、2a,2b,2c成等差数列 |
| D、2a,2b,2c成等比数列 |
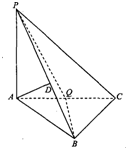 在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,
在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,