题目内容
设[m]表示不超过实数m的最大整数，则在直角坐标平面xOy上，则满足[x]2+[y]2=50的点P（x，y）所成的图形面积为 ．
考点：分段函数的应用
专题：函数的性质及应用
分析：根据方程可得对于x，y≥0时，求出x，y的整数解，可得|[x]|可能取的数值为7、5、1，则可以确定x的范围，进而得到对应的y的范围，求出面积即可．
解答：
解：由题意可得：方程：[x]2+[y]2=50
当x，y≥0时，[x]，[y]的整解有三组，（7，1），（5，5），（1，7）所以此时|[x]|可能取的数值为：7，5，1．
当|[x]|=7时，7≤x＜8，或-7≤x＜-6，|[y]|=1，-1≤y＜0，或1≤y＜2，围成的区域是4个单位正方形；
当|[x]|=5时，5≤x＜6，或-5≤x＜-4；|[y]|=5，-5≤y＜-4，5≤y＜6，围成的区域是4个单位正方形；
当|[x]|=1时，-1≤x＜0，或1＜x≤2，|[y]|=7，-7≤y＜-6，或7≤y＜8，围成的区域是4个单位正方形．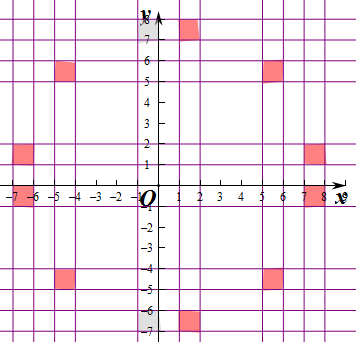
所以总面积是：12
故答案是12．
当x，y≥0时，[x]，[y]的整解有三组，（7，1），（5，5），（1，7）所以此时|[x]|可能取的数值为：7，5，1．
当|[x]|=7时，7≤x＜8，或-7≤x＜-6，|[y]|=1，-1≤y＜0，或1≤y＜2，围成的区域是4个单位正方形；
当|[x]|=5时，5≤x＜6，或-5≤x＜-4；|[y]|=5，-5≤y＜-4，5≤y＜6，围成的区域是4个单位正方形；
当|[x]|=1时，-1≤x＜0，或1＜x≤2，|[y]|=7，-7≤y＜-6，或7≤y＜8，围成的区域是4个单位正方形．
所以总面积是：12
故答案是12．
点评：本题考查探究性问题，是创新题，考查学生分析问题，解决问题的能力，而利用分类讨论和数形结合思想是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的2倍，且经过点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），l交椭圆于A、B两个不同点．