题目内容
函数f(x)=
+lg(3x+1)的定义域为( )
| 2x2 | ||
|
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-∞,
|
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据二次根式的定义及分母不为0可知1-x>0且根据对数函数定义得3x+1>0,联立求出解集即可.
解答:
解:要使函数有意义,x应满足:
解得:-
<x<1
故函数f(x)=
+lg(3x+1)的定义域为(-
,1)
故选:A
|
解得:-
| 1 |
| 3 |
故函数f(x)=
| 2x2 | ||
|
| 1 |
| 3 |
故选:A
点评:考查学生理解函数的定义域是指使函数式有意义的自变量x的取值范围.应会求不等式的解集.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
对数列{an},{bn},若区间[an,bn]满足下列条件:
①[an+1,bn+1]?[an,bn](n∈N*);
②
(bn-an)=0,
则称{[an,bn]}为区间套.下列选项中,可以构成区间套的数列是( )
①[an+1,bn+1]?[an,bn](n∈N*);
②
| lim |
| n→∞ |
则称{[an,bn]}为区间套.下列选项中,可以构成区间套的数列是( )
A、an=(
| ||||
B、an=(
| ||||
C、an=
| ||||
D、an=
|
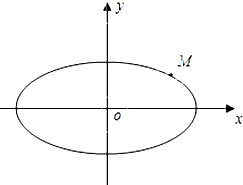 已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍,且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍,且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.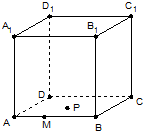 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=