题目内容
已知函数f(x)=ex,(x∈R)
(1)求f(x)在点(1,e)处的切线方程;
(2)证明:曲线y=f(x)与曲线y=
x2+x+1有唯一公共点.
(1)求f(x)在点(1,e)处的切线方程;
(2)证明:曲线y=f(x)与曲线y=
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)求函数的导数,利用导数的几何意义即可求f(x)在点(1,e)处的切线方程;
(2)构造函数h(x)=f(x)-(
x2+x+1)=ex-
x2-x-1,利用导数判断函数的单调性即可证明:曲线y=f(x)与曲线y=
x2+x+1有唯一公共点.
(2)构造函数h(x)=f(x)-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)函数的导数f′(x)=ex,则f′(1)=e,
则f(x)点(1,e)处的切线方程为:y-e=e(x-1),
即y=ex.
(2)令h(x)=f(x)-(
x2+x+1)=ex-
x2-x-1,
则h′(x)=ex-x-1,
[h′(x)]′=ex-1,且h(0)=0,h′(0)=0,[h′(0)]′=0,
因此,当x<0时,[h′(x)]′<0,y=h′(x)单调递减;
当x>0时,[h′(x)]′>0,y=h′(x)单调递增.
所以y=h′(x)≥h′(0)=0,
所以y=h(x)在R上单调递增,
又h(0)=0,即函数h(x)有唯一零点,
故曲线y=f(x)与曲线y=
x2+x+1有唯一公共点(0,1).
则f(x)点(1,e)处的切线方程为:y-e=e(x-1),
即y=ex.
(2)令h(x)=f(x)-(
| 1 |
| 2 |
| 1 |
| 2 |
则h′(x)=ex-x-1,
[h′(x)]′=ex-1,且h(0)=0,h′(0)=0,[h′(0)]′=0,
因此,当x<0时,[h′(x)]′<0,y=h′(x)单调递减;
当x>0时,[h′(x)]′>0,y=h′(x)单调递增.
所以y=h′(x)≥h′(0)=0,
所以y=h(x)在R上单调递增,
又h(0)=0,即函数h(x)有唯一零点,
故曲线y=f(x)与曲线y=
| 1 |
| 2 |
点评:本题主要考查导数的综合应用,利用导数求函数的切线以及构造函数判断函数的单调性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
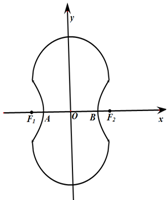 如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶
如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶