题目内容
点M(x,y)到定点F1(2,0)的距离和它到定直线l:x=8的距离的比是常数
.
(1)求点M的轨迹C;
(2)求过F2(-2,0)且倾斜角为45°的直线被曲线C所截的弦长.
| 1 |
| 2 |
(1)求点M的轨迹C;
(2)求过F2(-2,0)且倾斜角为45°的直线被曲线C所截的弦长.
考点:轨迹方程,直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设动点M(x,y),由圆锥曲线的共同性质知
=
,化简得点M的轨迹C;
(2)设出直线方程与椭圆方程联立,结合焦半径公式,即可求出过F2(-2,0)且倾斜角为45°的直线被曲线C所截的弦长.
| ||
| |8-x| |
| 1 |
| 2 |
(2)设出直线方程与椭圆方程联立,结合焦半径公式,即可求出过F2(-2,0)且倾斜角为45°的直线被曲线C所截的弦长.
解答:
解:(1)设动点M(x,y),由圆锥曲线的共同性质知
=
,
化简得:
+
=1;
(2)椭圆的另一焦点为F2(-2,0),过F2(-2,0)的倾斜角为45°的直线方程为y=x+2,
与椭圆方程联立得7x2+16x-32=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
,
由焦半径公式AB=a+ex1+a+ex2=2a+e(x1+x2)=8+
(-
)=
.
| ||
| |8-x| |
| 1 |
| 2 |
化简得:
| x2 |
| 16 |
| y2 |
| 12 |
(2)椭圆的另一焦点为F2(-2,0),过F2(-2,0)的倾斜角为45°的直线方程为y=x+2,
与椭圆方程联立得7x2+16x-32=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
| 16 |
| 7 |
由焦半径公式AB=a+ex1+a+ex2=2a+e(x1+x2)=8+
| 1 |
| 2 |
| 16 |
| 7 |
| 48 |
| 7 |
点评:本题考查轨迹方程的求法,考查了椭圆的方程,考查直线与椭圆的位置关系,是中档题.

练习册系列答案
相关题目
设甲、乙两楼相距20m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是( )
A、20
| ||||||||
B、10
| ||||||||
C、10(
| ||||||||
D、
|
如图是5名学生一次数学测试成绩的茎叶图,则这5名学生该次测试成绩的方差为( )


| A、20 | B、21.2 |
| C、106 | D、127 |
在△ABC中,若最大角的正弦值是
,则△ABC必是( )
| ||
| 2 |
| A、等边三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
 如图,在几何体ABC-A1B1C1中,点A1,B1,C1在平面ABC内的正投影分别为A,B,C,且AB⊥BC,E为AB1中点,AB=AA1=BB1=2CC1.
如图,在几何体ABC-A1B1C1中,点A1,B1,C1在平面ABC内的正投影分别为A,B,C,且AB⊥BC,E为AB1中点,AB=AA1=BB1=2CC1.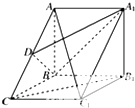 如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.