Question

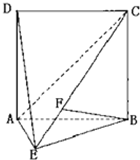如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．
（Ⅰ）求证：AE⊥平面BCE；
（Ⅱ）求二面角B-AC-E的余弦值；
（Ⅲ）求点D到平面ACE的距离．

Answer 1

考点：用空间向量求平面间的夹角,直线与平面垂直的判定,点、线、面间的距离计算

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）欲证AE⊥平面BCE，由题设条件知可先证BF⊥AE，CB⊥AE，再由线面垂直的判定定理得出线面垂直即可；
（Ⅱ）求二面角B-AC-E的正弦值，需要先作角，连接BD交AC交于G，连接FG，可证得∠BGF是二面B-AC-E的平面角，在△BFG中求解即可；
（Ⅲ）由题设，利用由V_D-ACE=V_E-ACD，求点D到平面ACE的距离．

解答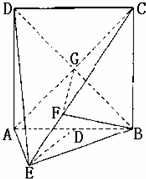： 解：（Ⅰ）∵BF⊥平面ACE．∴BF⊥AE
∵二面角D-AB-E为直二面角．且CB⊥AB．
∴CB⊥平面ABE∴CB⊥AE
∵BF∩CB=B
∴AE⊥平面BCE（4分）
（Ⅱ）连接BD交AC交于G，连接FG
∵正方形ABCD边长为2．∴BG⊥AC，BG=

2

∵BF⊥平面ACE．由三垂线定理的逆定理得FG⊥AC．
∴∠BGF是二面B-AC-E的平面角（7分）
∵AE⊥平面BCE，∴AE⊥EC
又∵AE=EB，∴在等腰直角三角形AEB中，BE=

2

又∵Rt△BCE中，EC=

6

∴BF=

BC×BE

EC

=

2 3

3

∴Rt△BFG中sin∠BGF=

BF

FG

=

6

3

∴二面角B-AC-E的正弦值等于

6

3

（10分）
（Ⅲ）过点E作EO⊥AB交AB于点O，OE=1
∵二面角D-AB-E为直二面角，∴EO⊥平面ABCD
设D到平面ACE的距离为h，由V_D-ACE=V_E-ACD，可得h=

1 2 AD•DC•EO

1 2 AE•EC

=

2 3

3

   …（13分）
∴点D到平面ACE的距离为

2 3

3

．        …（14分）

点评：本题考查了用线面垂直的判定定理证明线面垂直，以及用二面角的定义求二面角，求棱锥的体积，本题涉及到的知识与技巧较多，综合性较强，在解题过程中要注意体会问题的转化方向，及解决方法．