题目内容

在边长为a的菱形ABCD中，∠ABC=120°，PC⊥平面ABCD，E是PA中点，求E到平面PBC的距离．
考点：点、线、面间的距离计算
专题：综合题,空间位置关系与距离
分析：先根据直线与平面平行的判定定理可知只需证EF与平面PBC内一直线平行，而EF∥PB，又EF?平面PBC，PB?平面PBC证明EF∥平面PBC，再在面ABCD内作过F作FH⊥BC于H，又EF∥平面PBC，故点E到平面PBC的距离等于点F到平面PBC的距离FH．在直角三角形FBH中，求出FH即可，最后根据点E到平面PBC的距离等于点F到平面PBC的距离即可求出所求．
解答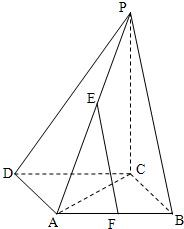： 解：∵AE=PE，AF=BF，
∴EF∥PB
又EF?平面PBC，PB?平面PBC，
故EF∥平面PBC
在面ABCD内作过F作FH⊥BC于H
∵PC⊥面ABCD，PC?面PBC
∴面PBC⊥面ABCD
又面PBC∩面ABCD=BC，FH⊥BC，FH?面ABCD，∴FH⊥面PBC
又EF∥平面PBC，故点E到平面PBC的距离等于点F到平面PBC的距离FH．
在直角三角形FBH中，∠FBC=120°，FB=
a
2
，FH=FBsin∠FBH=
3
4
a，
故点E到平面PBC的距离等于点F到平面PBC的距离等于
3
4
a．
点评：本题主要考查了直线与平面平行的判定，以及点到平面的距离，同时考查了空间想象能力，以及转化与划归的思想，属于中档题．
练习册系列答案
相关题目
作出函数y=|3x-1|的图象，并利用数形结合的方法研究方程|3x-1|=k的根的个数．
已知过点 M（
p
2
，0）的直线 l与抛物线 y2=2px（p＞0）交于A，B两点，且 
OA
•
OB
=-3，其中O为坐标原点．
（1）求p的值；
（2）若圆x2+y2-2x=0与直线l相交于以C，D（A，C两点均在第一象银），且线段AC，CD，DB长构成等差数列，求直线l的方程．
已知线段AB的两个端点A、B分别在x轴、y轴上滑动，|AB|=3，点M满足2
AM
=
MB
．
（1）求动点M的轨迹E的方程；
（2）若曲线E的所有弦都不能被直线l：y=k（x-1）垂直平分，求实数k的取值范围．
在平面直角坐标系xOy中，椭圆E的中心为原点，焦点F1，F2在y轴上，离心率为
3
3
．过F1的直线l交E于A，B两点，且△ABF2的周长为4
3
．
（1）求椭圆E的方程；
（2）过圆O：x2+y2=5上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证两切线斜率之积为定值．
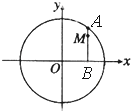如图，设A是圆x2+y2=6上的动点，点B是A在x轴上投影，M为AB上一点，且|MB|=
3
3
|AB|．当A在圆上运动时，点M的轨迹为曲线G．过点（m，0）（m＞
6
）且倾斜角为
5π
6
的直线l交曲线G于C，D两点．
（1）求曲线G的方程；
（2）若点F是曲线G的右焦点且∠CFD∈[
π
3
，
π
2
]，求m的取值范围．
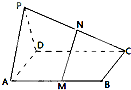如图，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB，PC的中点
（1）求证：MN∥平面PAD；
（2）若△PAD为正三角形，求异面直线PA与MN所成的角的大小．
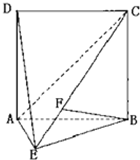如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．
（Ⅰ）求证：AE⊥平面BCE；
（Ⅱ）求二面角B-AC-E的余弦值；
（Ⅲ）求点D到平面ACE的距离．
函数f（x）=ax3-3x2+1在区间[
1
2
，2]上存在唯一零点，则实数a取值范围
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网