题目内容
已知数列{xn}的各项为不等于1的正数,其前n项和为Sn,点Pn的坐标为(xn,Sn),若所有这样的点Pn(n=1,2,…)都在斜率为k的同一直线(常数k≠0,1)上.
(Ⅰ)求证:数列{xn}是等比数列;
(Ⅱ)设yn=logxn2a2-3a+1满足ys=
,yt=
(s,t∈N,且s≠t)共中a为常数,且1<a<
,试判断,是否存在自然数M,使当n>M时,xn>1恒成立?若存在,求出相应的M;若不存在,请说明理由.
(Ⅰ)求证:数列{xn}是等比数列;
(Ⅱ)设yn=logxn2a2-3a+1满足ys=
| 1 |
| 2t+1 |
| 1 |
| 2s+1 |
| 3 |
| 2 |
考点:数列与不等式的综合,等比关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)由已知得(k-1)xn+1=kxn,由此能证明{xn}是公比为
的等比数列.
(Ⅱ)存在自然数M,使当n>M时,xn>1恒成立,由1<a<
,得0<2a2-3a+1<1,设公比为q>0首项为x1,则xn=x1•qn-1,得{
}是以d为公差的等差数列.从而推导出当n>M=(t+s)时,xn=(2a2-3a+1)
>1恒成立.
| k |
| k-1 |
(Ⅱ)存在自然数M,使当n>M时,xn>1恒成立,由1<a<
| 3 |
| 2 |
| 1 |
| yn |
| 1 |
| yn |
解答:
(Ⅰ)证明:∵点pn,pn+1都在斜率为k的直线上,
∴
=k,即
=k,…(1分)
故(k-1)xn+1=kxn
∵k≠0,xn+1≠1,xn≠1,…(3分)
∴
=
=常数,∴{xn}是公比为
的等比数列.…(4分)
(Ⅱ)解:答案是肯定的,即存在自然数M,使当n>M时,xn>1恒成立.…(5分)
事实上,由1<a<
,得0<2a2-3a+1<1 …(6分)
∵yn=log xn(2a2-3a+1),
∴
=log (2a2-3a+1)xn …(8分)
由(1)得{xn}是等比数列,设公比为q>0首项为x1,则xn=x1•qn-1(n∈N)
∴
=(n-1)log (2a2-3a+1)q+log (2a2-3a+1)x1
令d=log (2a2-3a+1)q,故得{
}是以d为公差的等差数列.
又∵
=2t+1,
=2s+1,
∴
-
=2(t-s)
即(s-1)d-(t-1)d=2(t-s),
∴d=-2…(10分)
故
=
+(n-s)(-2)=2(t+s)-2n+1(n∈N)
又∵xn=(2a2-3a+1)
,(n∈N)
∴要使xn>1恒成立,即须
<0…(12分)
∴2(t+s)-2n+1<0,∴n>(t+s)+
,
当M=t+s,n>M时,我们有
<0恒成立,
∵0<2a2-3a+1<1,
∴当n>M=(t+s)时,xn=(2a2-3a+1)
>1恒成立.…(14分)
∴
| Sn+1-Sn |
| xn+1-xn |
| xn+1 |
| xn+1-xn |
故(k-1)xn+1=kxn
∵k≠0,xn+1≠1,xn≠1,…(3分)
∴
| xn+1 |
| xn |
| k |
| k-1 |
| k |
| k-1 |
(Ⅱ)解:答案是肯定的,即存在自然数M,使当n>M时,xn>1恒成立.…(5分)
事实上,由1<a<
| 3 |
| 2 |
∵yn=log xn(2a2-3a+1),
∴
| 1 |
| yn |
由(1)得{xn}是等比数列,设公比为q>0首项为x1,则xn=x1•qn-1(n∈N)
∴
| 1 |
| yn |
令d=log (2a2-3a+1)q,故得{
| 1 |
| yn |
又∵
| 1 |
| ys |
| 1 |
| yt |
∴
| 1 |
| ys |
| 1 |
| yt |
即(s-1)d-(t-1)d=2(t-s),
∴d=-2…(10分)
故
| 1 |
| yn |
| 1 |
| ys |
又∵xn=(2a2-3a+1)
| 1 |
| yn |
∴要使xn>1恒成立,即须
| 1 |
| yn |
∴2(t+s)-2n+1<0,∴n>(t+s)+
| 1 |
| 2 |
当M=t+s,n>M时,我们有
| 1 |
| yn |
∵0<2a2-3a+1<1,
∴当n>M=(t+s)时,xn=(2a2-3a+1)
| 1 |
| yn |
点评:本题考查数列是等比数列的证明,考查满足条件的自然数是否存在的判断与求法,解题时要注意构造法的合理运用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
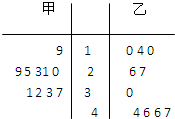 某林管部门在每年植树节前,为保证树苗的质量,都会对树苗进行检测.现从甲、乙两种树苗中各抽取10株,测量其高度,所得数据如茎叶图所示,则下列描述正确的是( )
某林管部门在每年植树节前,为保证树苗的质量,都会对树苗进行检测.现从甲、乙两种树苗中各抽取10株,测量其高度,所得数据如茎叶图所示,则下列描述正确的是( )| A、甲树苗的平均高度大于乙树苗的平均高度,且甲树苗比乙树苗长得整齐 |
| B、甲树苗的平均高度大于乙树苗的平均高度,但乙树苗比甲树苗长得整齐 |
| C、乙树苗的平均高度大于甲树苗的平均高度,但甲树苗比乙树苗长得整齐 |
| D、乙树苗的平均高度大于甲树苗的平均高度,且乙树苗比甲树苗长得整齐 |
下面四个推导过程符合演绎推理三段论形式且推理正确的是( )
| A、大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数 |
| B、大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数 |
| C、大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数 |
| D、大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数 |
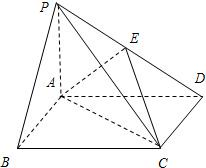 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.E是PD的中点,
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.E是PD的中点,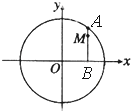 如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=
如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=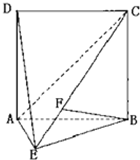 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.