题目内容
若实数x,y满足方程x2+y2-4x+1=0,则
的最大值为 ,最小值为 .
| y |
| x+1 |
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:整理方程可知,方程表示以点(2,0)为圆心,以
为半径的圆,设
=k,即kx-y+k=0,进而根据圆心(2,0)到kx-y+k=0的距离为半径时直线与圆相切,斜率取得最大、最小值,即可得出结论.
| 3 |
| y |
| x+1 |
解答:
 解:方程x2+y2-4x+1=0表示以点(2,0)为圆心,以
解:方程x2+y2-4x+1=0表示以点(2,0)为圆心,以
为半径的圆.
设
=k,即kx-y+k=0,
由圆心(2,0)到kx-y+k=0的距离为半径时直线与圆相切,斜率取得最大、最小值.
由
=
,
解得k2=
.
所以kmax=
,kmin=-
.
故答案为:
,-
.
 解:方程x2+y2-4x+1=0表示以点(2,0)为圆心,以
解:方程x2+y2-4x+1=0表示以点(2,0)为圆心,以| 3 |
设
| y |
| x+1 |
由圆心(2,0)到kx-y+k=0的距离为半径时直线与圆相切,斜率取得最大、最小值.
由
| |3k| | ||
|
| 3 |
解得k2=
| 1 |
| 2 |
所以kmax=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了圆的方程的综合运用.考查了学生转化和化归的思想和数形结合的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面四个推导过程符合演绎推理三段论形式且推理正确的是( )
| A、大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数 |
| B、大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数 |
| C、大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数 |
| D、大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数 |
到空间不共面的四点距离相等的平面的个数为( )
| A、1个 | B、4个 | C、7个 | D、8个 |
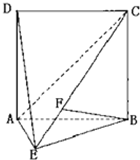 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.