题目内容
三棱柱 ABC-A1B1C1′中,∠ABC=90°,AA1=AC=BC=2,A1在底面ABC内的射影为AC的中点D.
(1)求证:BA1⊥AC1;
(2)求三棱锥 B1-A1DB的体积.
(1)求证:BA1⊥AC1;
(2)求三棱锥 B1-A1DB的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)根据直线平面的垂直得出BC⊥AC1,再判断出四边形ACC1A1为菱形,即AC1⊥A1C,运用判断定理可得得证AC1⊥平面A1BC,BA1⊥AC1,
(2)转化体积问题)V B1-A1DB=V B-A1B1D=V D-A1BB1=
V C1-A1B1B=
VB-A1B1C=
V ABC-A1B1C1运用体积公式求解即可.
(2)转化体积问题)V B1-A1DB=V B-A1B1D=V D-A1BB1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
解答:
(1)证明:∵A1D⊥平面ABC,A1D?平面ACC1A1,
∴平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,
∵BC?平面ABC,BC⊥AC,
∴BC⊥平面ACC1A1,
∴BC⊥AC1,
∵AA1=CA,
∴四边形ACC1A1为菱形,即AC1⊥A1C,
∵A1C,BC?平面A1BC,A1C∩BC=C,
∴AC1⊥平面A1BC,
∵BA1?平面A1BC,
∴BA1⊥AC1,
(2)V B1-A1DB=V B-A1B1D=V D-A1BB1=
V C1-A1B1B=
VB-A1B1C=
V ABC-A1B1C1=
×2×2×
×
=
∴平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,
∵BC?平面ABC,BC⊥AC,
∴BC⊥平面ACC1A1,
∴BC⊥AC1,
∵AA1=CA,
∴四边形ACC1A1为菱形,即AC1⊥A1C,
∵A1C,BC?平面A1BC,A1C∩BC=C,
∴AC1⊥平面A1BC,
∵BA1?平面A1BC,
∴BA1⊥AC1,
(2)V B1-A1DB=V B-A1B1D=V D-A1BB1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
点评:本题考查了空间几何体的性质,运用直线平面的垂直的判断,性质,解决问题,求解体积,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下面四个推导过程符合演绎推理三段论形式且推理正确的是( )
| A、大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数 |
| B、大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数 |
| C、大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数 |
| D、大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数 |
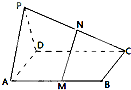 如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB,PC的中点
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB,PC的中点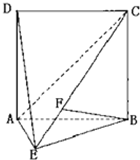 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.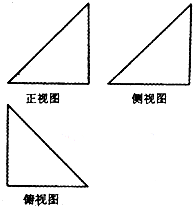 如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为
如图,某几何体的三视图均为腰长为1的等腰直角三角形,则此几何体最长的棱长为