题目内容
已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,PC与平面PAD所成角的正弦值为
,E、F分别是AB、PC的中点,PA⊥平面ABCD.
(1)求证:EF∥平面PAD;
(2)求PA的长.
| ||
| 4 |
(1)求证:EF∥平面PAD;
(2)求PA的长.
考点:直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)取PD的中点M,连接AM,FM,由MF∥CD∥AE,MF=AE=1,可得AEMF是平行四边形,从而证明EF∥平面PAD;
(2)作CH⊥AD于H点,可证CH⊥PH,可得sin∠HPC=
=
,可得CH=
,HD=1,AH=1,有由sin∠HPC=
=
可解得PC=2
,可得PH=
,即可求得PA的值.
(2)作CH⊥AD于H点,可证CH⊥PH,可得sin∠HPC=
| ||
| 4 |
| HC |
| PC |
| 3 |
| ||
| 4 |
| HC |
| PC |
| 2 |
| 5 |
解答:
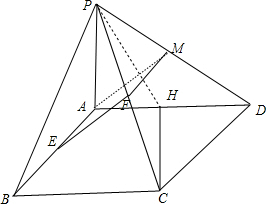 证明:(1)取PD的中点M,连接AM,FM,
证明:(1)取PD的中点M,连接AM,FM,
∵底面ABCD是边长为2的菱形,E、F分别是AB、PC的中点,
∴MF∥CD∥AE,MF=AE=1,
∴AEMF是平行四边形,EF∥AM,
∵AM?平面PAD,EF?平面PAD,
∴EF∥平面PAD;
(2)作CH⊥AD于H点,
∵PA⊥平面ABCD.∴PA⊥CH,
∴CH⊥平面PAD,
∴CH⊥PH,
∵PC与平面PAD所成角的正弦值为
,则sin∠HPC=
=
,
∵底面ABCD是边长为2的菱形,∠ABC=60°,
∴CH=
,HD=1,AH=1,
∴由sin∠HPC=
=
可解得PC=2
,
∴PH=
=
,
∴PA=
=2.
 证明:(1)取PD的中点M,连接AM,FM,
证明:(1)取PD的中点M,连接AM,FM,∵底面ABCD是边长为2的菱形,E、F分别是AB、PC的中点,
∴MF∥CD∥AE,MF=AE=1,
∴AEMF是平行四边形,EF∥AM,
∵AM?平面PAD,EF?平面PAD,
∴EF∥平面PAD;
(2)作CH⊥AD于H点,
∵PA⊥平面ABCD.∴PA⊥CH,
∴CH⊥平面PAD,
∴CH⊥PH,
∵PC与平面PAD所成角的正弦值为
| ||
| 4 |
| ||
| 4 |
| HC |
| PC |
∵底面ABCD是边长为2的菱形,∠ABC=60°,
∴CH=
| 3 |
∴由sin∠HPC=
| ||
| 4 |
| HC |
| PC |
| 2 |
∴PH=
| PC2-CH2 |
| 5 |
∴PA=
| PH2-AH2 |
点评:本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,属于基本知识的考查.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
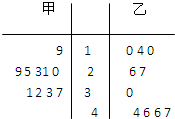 某林管部门在每年植树节前,为保证树苗的质量,都会对树苗进行检测.现从甲、乙两种树苗中各抽取10株,测量其高度,所得数据如茎叶图所示,则下列描述正确的是( )
某林管部门在每年植树节前,为保证树苗的质量,都会对树苗进行检测.现从甲、乙两种树苗中各抽取10株,测量其高度,所得数据如茎叶图所示,则下列描述正确的是( )| A、甲树苗的平均高度大于乙树苗的平均高度,且甲树苗比乙树苗长得整齐 |
| B、甲树苗的平均高度大于乙树苗的平均高度,但乙树苗比甲树苗长得整齐 |
| C、乙树苗的平均高度大于甲树苗的平均高度,但甲树苗比乙树苗长得整齐 |
| D、乙树苗的平均高度大于甲树苗的平均高度,且乙树苗比甲树苗长得整齐 |
下面四个推导过程符合演绎推理三段论形式且推理正确的是( )
| A、大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数 |
| B、大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数 |
| C、大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数 |
| D、大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数 |
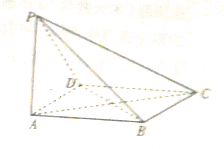 如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.
如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.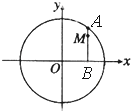 如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=
如图,设A是圆x2+y2=6上的动点,点B是A在x轴上投影,M为AB上一点,且|MB|=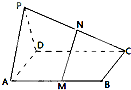 如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB,PC的中点
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB,PC的中点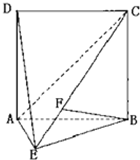 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.