题目内容
在坐标平面内，不等式组
所表示的平面区域的面积为（ ）
|
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点：简单线性规划
专题：不等式的解法及应用
分析：先画出满足条件的平面区域，从而求出三角形的面积．
解答：
解：画出满足条件的平面区域，如图示：
，
不等式组表示的平面区域是以（0，0），（-1，1），（0，2）为顶点的三角形，
其面积为S=
×2×1=1．
故选：B．
，不等式组表示的平面区域是以（0，0），（-1，1），（0，2）为顶点的三角形，
其面积为S=
| 1 |
| 2 |
故选：B．
点评：本题考查了简单的线性规划问题，考查了数形结合思想，是一道基础题．
练习册系列答案
全能练考卷系列答案
相关题目
若（1+2ai）i=1-bi，其中a、b∈R，i是虚数单位，则|a+bi|=（ ）
A、
| ||||
| B、5 | ||||
C、
| ||||
D、
|
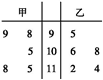在某中学举行的跳高比赛选拨赛中，甲和乙进行了5次比赛，他们的成绩用如图所示的茎叶图表示，则下列说法正确的是（ ）| A、甲的平均成绩比乙的平均成绩高，甲比乙成绩稳定 |
| B、甲的平均成绩比乙的平均成绩低，乙比甲成绩稳定 |
| C、甲的平均成绩与乙的平均成绩一样，但甲比乙成绩稳定 |
| D、甲的平均成绩与乙的平均成绩一样，但乙比甲成绩稳定 |
已知命题p：π是无理数；命题q：π是有理数；则以下命题中的假命题是（ ）
| A、p或q | B、p且￢q |
| C、￢p或￢q | D、￢p且q |
已知函数f（x）=4x-2x+1+1，函数g（x）=asin（
x）-2a+2（a＞0），若存在x1，x2∈[0，1]，使得f（x1）=g（x2）成立，则实数a的取值范围是（ ）
| π |
| 6 |
A、（0，
| ||||
B、[
| ||||
C、[
| ||||
D、[
|