题目内容

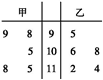在某中学举行的跳高比赛选拨赛中，甲和乙进行了5次比赛，他们的成绩用如图所示的茎叶图表示，则下列说法正确的是（　　）
A、甲的平均成绩比乙的平均成绩高，甲比乙成绩稳定
B、甲的平均成绩比乙的平均成绩低，乙比甲成绩稳定
C、甲的平均成绩与乙的平均成绩一样，但甲比乙成绩稳定
D、甲的平均成绩与乙的平均成绩一样，但乙比甲成绩稳定
考点：茎叶图
专题：概率与统计
分析：分别求出甲乙的平均成绩，并计算方差，从而得到答案．
解答： 解：
.
x
甲=
1
5
（98+99+105+115+118）=107，
.
x
乙=
1
5
（95+106+108+112+114）=107，
S
2
甲
=
1
5
[（98-107）2+（99-107）2+（105-107）2+（115-107）2+（118-107）2]=66.8，
S
2
乙
=
1
5
[（95-107）2+（106-107）2+（108-107）2+（112-107）2+（114-107）2]=44．
故选：D
点评：本题考查了茎叶图问题，考查了平均数，方差问题，是一道基础题．
练习册系列答案
相关题目
下列命题中，假命题为（　　）
A、若
a
-
b
=
0
，则
a
=
b
B、若
a
•
b
=0，则
a
=
0
或
b
=
0
C、若k∈R，k
a
=
0
，则k=0或 
a
=
0
D、若
a
，
b
都是单位向量，则
a
•
b
≤1恒成立
设f（x）是一次函数，已知f（8）=15，且f（2），f（5），f（4）成等比数列．
（1）求f（x）的解析式；
（2）求f（2）+f（4）+f（6）+…+f（2n）．
已知数列{an}的前n项和为Sn，且Sn+an=1（n∈N*），等差数列{bn}的公差为正数，其前n项和为Tn，T3=15，且b1，
1
a2
，b3成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若cn=
3
bnbn+1
，求数列{cn}的前n项和Pn．
若方程
x2
3-k
-
y2
k-1
=1表示双曲线，则实数k的取值范围是（　　）
A、k＜1B、1＜k＜3
C、k＞3D、k＜1或k＞3
在坐标平面内，不等式组
y≥|x|
y≤x+2
x≤0
所表示的平面区域的面积为（　　）
A、
1
2
B、1
C、
2
D、2
已知函数f（x）=
ax2+1
bx+c
（a，c∈R，b∈N，a＞0，b＞0）是奇函数，在区间（0，+∞）上，函数有最小值2，且f（1）＜
5
2
．
（1）求f（x）的解析式．
（2）函数f（x）图象上是否存在两点关于点（1，0）对称？若存在，求出这些点的坐标；若不存在，说明理由．
已知数列{an}前n项和为Sn且Sn=3an+1，求{an}通项公式．
若cos（
π
3
-α）=
2
3
，α∈（-π，0），则sin（
π
3
+2α）=（　　）
A、
2
5
9
B、
4
5
9
C、-
2
5
9
D、-
4
5
9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网