题目内容
已知函数f(x)=(x+a)2-7bln x+1,其中a,b是常数且a≠0.
(1)若b=1时,f(x)在区间(1,+∞)上单调递增,求a的取值范围;
(2)当b=
a2时,讨论f(x)的单调性.
(1)若b=1时,f(x)在区间(1,+∞)上单调递增,求a的取值范围;
(2)当b=
| 4 |
| 7 |
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)先求出函数的导数,问题转化为a≥
-x在x>1时恒成立,通过讨论x的范围,从而求出a的范围;
(2)先求出函数的导数,通过讨论a的范围,从而求出函数的单调区间.
| 7 |
| 2x |
(2)先求出函数的导数,通过讨论a的范围,从而求出函数的单调区间.
解答:
解:(1)∵b=1,∴f(x)=(x+a)2-7lnx+1,
∴f′(x)=2x+2a-
.
∵当x>1时,f(x)是增函数,
∴f′(x)=2x+2a-
≥0在x>1时恒成立.
即a≥
-x在x>1时恒成立.
∵当x>1时,y=
-x是减函数,
∴当x>1时,y=
-x<
,∴a≥
.
(2)∵b=
a2,
∴f(x)=(x+a)2-4a2ln x+1,x∈(0,+∞).
∴f′(x)=
=
.
当a>0时,f′(x)>0,得x>a或x<-2a,
故f(x)的减区间为(0,a),增区间为(a,+∞);
当a<0时,f′(x)>0,得x>-2a或x<a,
故f(x)的减区间为(0,-2a),增区间为(-2a,+∞).
∴f′(x)=2x+2a-
| 7 |
| x |
∵当x>1时,f(x)是增函数,
∴f′(x)=2x+2a-
| 7 |
| x |
即a≥
| 7 |
| 2x |
∵当x>1时,y=
| 7 |
| 2x |
∴当x>1时,y=
| 7 |
| 2x |
| 5 |
| 2 |
| 5 |
| 2 |
(2)∵b=
| 4 |
| 7 |
∴f(x)=(x+a)2-4a2ln x+1,x∈(0,+∞).
∴f′(x)=
| 2x2+2ax-4a2 |
| x |
| 2(x-a)(x+2a) |
| x |
当a>0时,f′(x)>0,得x>a或x<-2a,
故f(x)的减区间为(0,a),增区间为(a,+∞);
当a<0时,f′(x)>0,得x>-2a或x<a,
故f(x)的减区间为(0,-2a),增区间为(-2a,+∞).
点评:本题考查了函数的单调性,考查了导数的应用,函数恒成立问题,考查转化思想,分类讨论思想,是一道中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
组合式
-2
+4
-8
+…+(-2)n
的值等于( )
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| A、(-1)n |
| B、1 |
| C、3n |
| D、3n-1 |
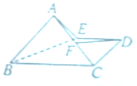 如图 所示的几何体ABCDE中,底面BCDE是∠C,∠D为直角的直角梯形,侧面ABE是∠A为直角的直角三角形,且AB=CD=6,BC=6
如图 所示的几何体ABCDE中,底面BCDE是∠C,∠D为直角的直角梯形,侧面ABE是∠A为直角的直角三角形,且AB=CD=6,BC=6