题目内容
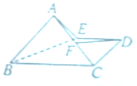 如图 所示的几何体ABCDE中,底面BCDE是∠C,∠D为直角的直角梯形,侧面ABE是∠A为直角的直角三角形,且AB=CD=6,BC=6
如图 所示的几何体ABCDE中,底面BCDE是∠C,∠D为直角的直角梯形,侧面ABE是∠A为直角的直角三角形,且AB=CD=6,BC=6| 2 |
| 2 |
(1)FD∥平面ABE;
(2)AC⊥BE.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)由题意可取AB中点为M,连接MF,ME,将证明FD∥平面ABE转化为证明DF∥ME即可;
(2)△ABE可看成是将矩形ABCD沿BE折叠得到,过A作垂线交BE于点G,则CG⊥BD,故BE⊥平面CG,即得AC⊥BE.
(2)△ABE可看成是将矩形ABCD沿BE折叠得到,过A作垂线交BE于点G,则CG⊥BD,故BE⊥平面CG,即得AC⊥BE.
解答:
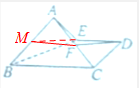 证明:(1)由题意,如右图,可取AB中点为M,连接MF,ME,
证明:(1)由题意,如右图,可取AB中点为M,连接MF,ME,
∵底面BCDE是∠C,∠D为直角的直角梯形,
∴ED∥BC,
又∵DE=3
,BC=6
,
∴ED=
BC,
∵M为AB的中点,
∴MF是△ABC的中位线,
即MF∥BC,MF=
BC,
所以MF平行且等于ED,
即四边形MFDE为平行四边形,从而ME平行DF,
又ME?平面ABE,FD?平面ABE
∴DF∥平面ABE.
(2))如右图△ABE沿BE展开至A、B、C、D四点在同一个平面上,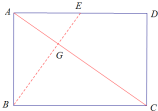
∵AB=CD=6,BC=6
,AE=DE=3
,
∠C,∠D为直角,∠A为直角,
∴平面四边形ABCD为矩形,
连结矩形ABCD的对角线AC交BE于G,则
•
=(
+
)•(
+
)
=-
2+
•
=-6×6+3
×6
=0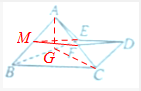 .
.
即
⊥
,故在矩形ABCD中有BE⊥AC,
由于翻折不改变此垂直关系,
所以在右图中,AG⊥BE,GC⊥BE,
故BE⊥平面AGC,
所以BE⊥AC.
 证明:(1)由题意,如右图,可取AB中点为M,连接MF,ME,
证明:(1)由题意,如右图,可取AB中点为M,连接MF,ME,∵底面BCDE是∠C,∠D为直角的直角梯形,
∴ED∥BC,
又∵DE=3
| 2 |
| 2 |
∴ED=
| 1 |
| 2 |
∵M为AB的中点,
∴MF是△ABC的中位线,
即MF∥BC,MF=
| 1 |
| 2 |
所以MF平行且等于ED,
即四边形MFDE为平行四边形,从而ME平行DF,
又ME?平面ABE,FD?平面ABE
∴DF∥平面ABE.
(2))如右图△ABE沿BE展开至A、B、C、D四点在同一个平面上,

∵AB=CD=6,BC=6
| 2 |
| 2 |
∠C,∠D为直角,∠A为直角,
∴平面四边形ABCD为矩形,
连结矩形ABCD的对角线AC交BE于G,则
| BE |
| AC |
| BA |
| AE |
| AB |
| BC |
=-
| AB |
| AE |
| BC |
=-6×6+3
| 2 |
| 2 |
=0
 .
.即
| BE |
| AC |
由于翻折不改变此垂直关系,
所以在右图中,AG⊥BE,GC⊥BE,
故BE⊥平面AGC,
所以BE⊥AC.
点评:本题考查线线垂直、线面平行的证明,是立体几何中常考的题型,作出恰当的辅助线是解题的关键,属难题.

练习册系列答案
相关题目
已知α,β均为锐角,sinα=
,cosβ=
,求α-β为( )
| ||
| 5 |
| ||
| 10 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
若二次函数y=x2-2x+1在区间(-∞,a]上为减函数,则a的取值范围是( )
| A、a>1 | B、a≥1 |
| C、a<1 | D、a≤1 |
 如图,在△ABC中,D为BC的中点,E为AD上任一点,且
如图,在△ABC中,D为BC的中点,E为AD上任一点,且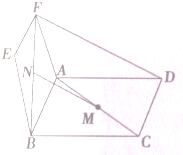 如图,已知?ABCD与?ABEF共边于AB,M,N分别在对角线AC,BF上,且AM:AC=FN:FB.求证:MN∥平面ADF.
如图,已知?ABCD与?ABEF共边于AB,M,N分别在对角线AC,BF上,且AM:AC=FN:FB.求证:MN∥平面ADF.