题目内容
求曲线y=5
与直线y=2x-4平行的切线的方程.
| x |
考点:利用导数研究曲线上某点切线方程
专题:导数的概念及应用,直线与圆
分析:求导数,利用曲线与直线y=2x-4平行,求出切点坐标,即可求出曲线与直线y=2x-4平行的切线的方程.
解答:
解:设切点为(m,n),
∵f(x)=5
,
∴f′(x)=
,
∵曲线与直线y=2x-4平行,
∴
=2,
解得m=
,则n=
,
∴曲线与直线y=2x-4平行的切线的方程为y-
=2(x-
),
即16x-8y+25=0.
∵f(x)=5
| x |
∴f′(x)=
| 5 | ||
2
|
∵曲线与直线y=2x-4平行,
∴
| 5 | ||
2
|
解得m=
| 25 |
| 16 |
| 25 |
| 4 |
∴曲线与直线y=2x-4平行的切线的方程为y-
| 25 |
| 4 |
| 25 |
| 16 |
即16x-8y+25=0.
点评:本题考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,正确求导和运用两直线平行的条件是解题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若二次函数y=x2-2x+1在区间(-∞,a]上为减函数,则a的取值范围是( )
| A、a>1 | B、a≥1 |
| C、a<1 | D、a≤1 |
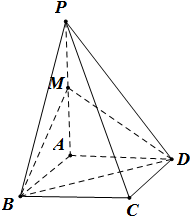 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠ABC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠ABC= 如图所示,已知在正方体ABCD-A1B1C1D1中,E是DD1的中点,求证:DB1∥平面A1C1E.
如图所示,已知在正方体ABCD-A1B1C1D1中,E是DD1的中点,求证:DB1∥平面A1C1E.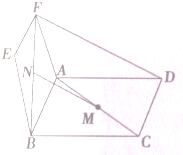 如图,已知?ABCD与?ABEF共边于AB,M,N分别在对角线AC,BF上,且AM:AC=FN:FB.求证:MN∥平面ADF.
如图,已知?ABCD与?ABEF共边于AB,M,N分别在对角线AC,BF上,且AM:AC=FN:FB.求证:MN∥平面ADF.