题目内容
已知圆O的方程为x2+y2=5.
(1)直线l过点A(4,0),且与圆O相切,求直线l的方程;
(2)直线l过点A(1,2),且与圆O相切,求直线l的方程.
(1)直线l过点A(4,0),且与圆O相切,求直线l的方程;
(2)直线l过点A(1,2),且与圆O相切,求直线l的方程.
考点:圆的切线方程
专题:计算题,直线与圆
分析:(1)求出圆的圆心为O(0,0),半径r=
.设方程为y=k(x-4),利用圆心O到直线的距离等于半径r,可得直线l的方程;
(2)设过P点的切线方程为y-2=k(x-1),利用点到直线的距离建立关于k的等式,解之得k=-
,即可得到所求圆的切线方程.
| 5 |
(2)设过P点的切线方程为y-2=k(x-1),利用点到直线的距离建立关于k的等式,解之得k=-
| 1 |
| 2 |
解答:
解:圆x2+y2=5的圆心为O(0,0),半径r=
.
(1)设方程为y=k(x-4),即kx-y-4k=0,
∵直线与圆x2+y2=5相切,
∴圆心O到直线的距离等于半径r,即d=
=
,
∴k=±
,
∴直线方程为y=±
(x-4);
(2)根据题意,可得过P(1,2)的切线斜率存在,设其方程为y-2=k(x-1),即kx-y+2-k=0.
∵直线与圆x2+y2=5相切,
∴圆心O到直线的距离等于半径r,即d=
=
,
化简整理得:4k2+4k-1=0,解之得k=-
,
∴直线方程为y-2=-
(x-1),化简得x+2y-5=0.
| 5 |
(1)设方程为y=k(x-4),即kx-y-4k=0,
∵直线与圆x2+y2=5相切,
∴圆心O到直线的距离等于半径r,即d=
| |-4k| | ||
|
| 5 |
∴k=±
| ||
| 11 |
∴直线方程为y=±
| ||
| 11 |
(2)根据题意,可得过P(1,2)的切线斜率存在,设其方程为y-2=k(x-1),即kx-y+2-k=0.
∵直线与圆x2+y2=5相切,
∴圆心O到直线的距离等于半径r,即d=
| |2-k| | ||
|
| 5 |
化简整理得:4k2+4k-1=0,解之得k=-
| 1 |
| 2 |
∴直线方程为y-2=-
| 1 |
| 2 |
点评:本题给出圆的方程,求圆经过定点的切线方程.着重考查了直线的方程、圆的标准方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
已知数列{an}中,an>0,a1=1,an+2=
,a100=a96,则a2014+a3=( )
| 1 |
| an+1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知α,β均为锐角,sinα=
,cosβ=
,求α-β为( )
| ||
| 5 |
| ||
| 10 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
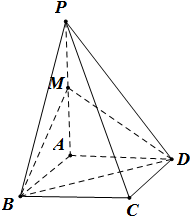 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠ABC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠ABC=