题目内容
已知函数f(x)=(cosx+sinx)(cosx-sinx).
(1)求函数f(x)的单调增区间;
(2)若0<α<
,0<β<
,且f(
)=
,f(
)=
,求sin(α-β)的值.
(1)求函数f(x)的单调增区间;
(2)若0<α<
| π |
| 2 |
| π |
| 2 |
| α |
| 2 |
| 1 |
| 3 |
| β |
| 2 |
| 2 |
| 3 |
考点:两角和与差的正弦函数,正弦函数的单调性
专题:三角函数的求值
分析:(1)利用二倍角公式化简函数解析式为f(x)=cos2x,令2kπ-π≤2x≤2kπ,求得x的范围,可得函数的增区间;令2kπ≤2x≤2kπ+π,求得x的范围,可得函数的减区间.
(2)由f(
)=
,f(
)=
,可得 cosα=
,cosβ=
.再结合α、β的范围,可得 sinα 和sinβ 的值,再根据sin(α-β)=sinαcosβ-cosαsinβ,计算求得结果.
(2)由f(
| α |
| 2 |
| 1 |
| 3 |
| β |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
解答:
解:(1)函数f(x)=(cosx+sinx)(cosx-sinx)=cos2x-sin2x=cos2x,
令2kπ-π≤2x≤2kπ,求得kπ-
≤x≤kπ,k∈z,
故函数的增区间为[kπ-
,kπ],k∈z.
令2kπ≤2x≤2kπ+π,求得kπ≤x≤kπ+
,k∈z,
故函数的减区间为[kπ,kπ+
],k∈z.
(2)由f(
)=
,f(
)=
,可得 cosα=
,cosβ=
.
再结合 0<α<
,0<β<
,可得 sinα=
,sinβ=
,
∴sin(α-β)=sinαcosβ-cosαsinβ=
×
-
×
=
.
令2kπ-π≤2x≤2kπ,求得kπ-
| π |
| 2 |
故函数的增区间为[kπ-
| π |
| 2 |
令2kπ≤2x≤2kπ+π,求得kπ≤x≤kπ+
| π |
| 2 |
故函数的减区间为[kπ,kπ+
| π |
| 2 |
(2)由f(
| α |
| 2 |
| 1 |
| 3 |
| β |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
再结合 0<α<
| π |
| 2 |
| π |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
∴sin(α-β)=sinαcosβ-cosαsinβ=
2
| ||
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
4
| ||||
| 9 |
点评:本题主要考查二倍角公式、余弦函数的单调性,同角三角函数的基本关系,两角差的正弦公式,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
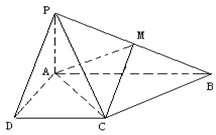 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= 气象台预报,距离S岛正东方向300km的A处有一台风形成,并以每小时30km的速度向北偏西30°的方向移动,在距台风中心处不超过270km以内的地区将受到台风的影响.问:
气象台预报,距离S岛正东方向300km的A处有一台风形成,并以每小时30km的速度向北偏西30°的方向移动,在距台风中心处不超过270km以内的地区将受到台风的影响.问: